Inscription / Connexion Nouveau Sujet
Bonjour,
Que ce soit pour le polygone intérieur ou extérieur, l' angle intercepté par un côté est le même.
Il vaut

Bonjour lake ! D'accord je comprend mieux car je me disais aussi que le nombre de côtés était le même pour le polygone intérieur et extérieur 😀 Pouvez vous m'aidez pour la question 2) b) ? Ce dm est vraiment compliqué et je ne comprend pas pourquoi mon professeur m'a donné cet exercice, en effet il s'agit d'un devoir maison pour les élèves étant le moins en difficultés mais aucun d'entre nous n'y arrivé 
Si j' ai l' aval de Jedoniezh, je peux continuer, oui...
Il y a quelques petites difficultés dans la partie 4)...

@Jedoniezh @lake en fait pour la question 2) b) je comprend juste le 3 x 2n qui représente le nombre de côtés et le  /(3 x 2n) qui représente en fait l'angle qui intercepte un côté mais divisé par 2 car pn et qn représente un demi-périmètre. Maintenant, je ne comprend pas l'expression dans son ensemble et d'où vienne le sin dans l'expression de pn et le tan dans l'expression de qn...
/(3 x 2n) qui représente en fait l'angle qui intercepte un côté mais divisé par 2 car pn et qn représente un demi-périmètre. Maintenant, je ne comprend pas l'expression dans son ensemble et d'où vienne le sin dans l'expression de pn et le tan dans l'expression de qn...
Vas y Lake je t'en prie.
J'étais partie sur une lancée mais ça s'est dilué dans le temps et je me suis perdu en route.
Je regarde de loin. 
2)b) Un dessin:
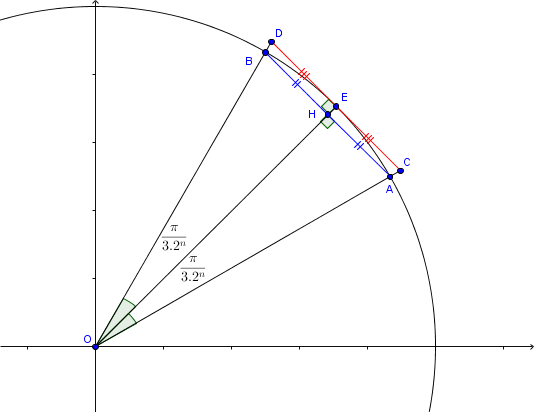
et
représentent respectivement un côté du polygone intérieur
et extérieur
puisque
donc
De la même manière:
puisque
donc
C' est un début; je n' aurai pas le temps cet après midi, mais je continuerai ce soir...

Bonsoir, je ne comprend pas comment vous passez de (1/2)(1/(3 x 2n x sin(an)) + 1/(3 x 2n x(sin(an))/(cos(an))) à (1/(3 x 2n+1)) ((1 + cosan)/sinan))?
4a) ,
donc et comme
c' est à dire
Avec , on obtient:
Soit
4)b) est une suite à termes positifs.
Avec 3)b), on sait que
donc
Mais comme , alors
On en déduit: ou si tu préfères:
Donc la suite est décroissante.
4)c) On sait d' après 4)a) que:
or d' après 3)b):
donc:
et comme
:
On en déduit:
Soit avec 3)b)
La suite est donc croissante.
4)d) On sait d' après 3)b) que
Donc
Or
donc
donc encore
On a donc bien
(croissance de
).
avec la question précédente.
(1)
On montre ensuite par récurrence que
Initialisation:
On a bien
La propriété est donc vraie au rang
Hérédité:
On suppose que la propriété est vraie pour un entier naturel fixé :
Alors, avec (1) et l' hypothèse de récurrence.
L' hérédité est prouvée pour tout :
4)e) On a
Le théorème dit des "gendarmes" permet d' affirmer que
De plus est croissante et
est décroissante.
Les deux suites sont donc adjacentes.
Elles sont donc convergentes et ont la même limite.
Le 5) plus tard...

je ne comprend pas comment vous passez de (1/2)(1/(3 x 2n x sin(an)) + 1/(3 x 2n x(sin(an))/(cos(an))) à (1/(3 x 2n+1)) ((1 + cosan)/sinan))?
On met

5a) Pour tout , on a
Avec , on obtient:
puis en multipliant par :
5)b) Soit
En passant à la limite dans la relation du 5)a), on obtient:
Donc
6) Un tableur et les relations de récurrences donnent pour :

D'accord je vais réfléchir et essayer de comprendre tout cela  Merci beaucoup pour votre aide et votre patience !!
Merci beaucoup pour votre aide et votre patience !!  et merci aussi à Jedoniezh pour m'avoir aiguillé au debut de mon DM !
et merci aussi à Jedoniezh pour m'avoir aiguillé au debut de mon DM !


