Inscription / Connexion Nouveau Sujet
Approximation de π par la méthode d'Archimède
Bonjour ! J'ai ce DM à faire pour la rentrée et je bloque dès la première question...
J'espère que quelqu'un pourra m'aider et je le remercie d'avance ! 
Énoncé :
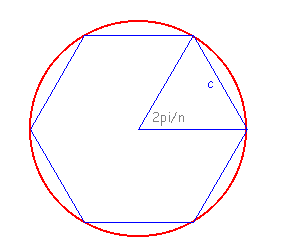
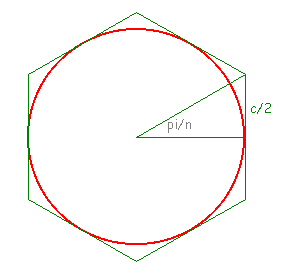
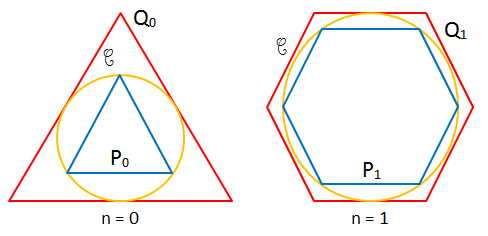
On considère un cercle C de rayon 1. Pour tout entier naturel n, on construit deux polygones réguliers Pn et Qn ayant chacun 3 x 2n côtés, Pn étant inscrit dans C et Qn étant exinscrit à C (voir figures ci-dessous).
On note pn et qn les demi-périmètres respectifs des polygones Pn et Qn.
1) Cas particuliers
a) Montrer que p0 = (3
3)/2 et q0 = 33 .
b) Calculer p1 et q1.
2) Expression de pn et qn
a) Exprimer, en fonction de n, l'angle au centre qui intercepte l'un des côtés de Pn ou de Qn.
b) En déduire que, pour tout entier naturel n, pn = 3 x 2n x sin(
/(3 x 2n)) et qn = 3 x 2n x tan(/(3 x 2n)).
3) Relation de récurrence
On pose an = /(3 x 2n).
a) Exprimer an en fonction de an+1 puis sin(an) et 1 + cos(an) en fonction de cos(an+1) et sin(an+1).
b) En déduire que, pour tout entier naturel n, (1/2)((1/pn) + (1/qn)) = 1/qn+1 et (pnqn+1) = pn+1.
4) Études des suites (pn) et (qn)
a) Montrer que, pour tout réel x 
[0 ; /2[, sin(x) 
tan(x).
En déduire que, pour tout entier naturel n, pn qn.
b) Montrer que la suite (qn) est décroissante.
c) Montrer que, pour tout entier naturel n, pn qn+1 et en déduire que la suite (pn) est croissante.
d) Montrer que, pour tout entier naturel n, qn+1 (1/2)(pn + qn) puis que qn+1 - pn+1 (1/2)(qn - pn).
En déduire que, pour entier naturel n, qn - pn (33)/2 x (1/2)n.
e) Démontrer que les suites (pn) et (qn) sont convergentes et ont la même limite.
5) Calcul de la limite commune
On admet que pour tout réel x [0 ; /2[, sin(x) x tan(x).
a) Montrer que, pour tout entier naturel n, pn qn.
b) En déduire la limite des suites (pn) et (qn).
6) Utilisation d'un tableur
À l'aide d'un tableur et des relations de récurrence, calculer les valeurs de pn et qn et donner un encadrement de d'amplitude 10-6.
Bonsoir !
J'ai déjà tracé les figures sur une feuille en traçant un cercle de rayon 1cm mais je ne vois pas en quoi cela peut m'aider pour la première question... Pouvez vous me donner une piste ? 
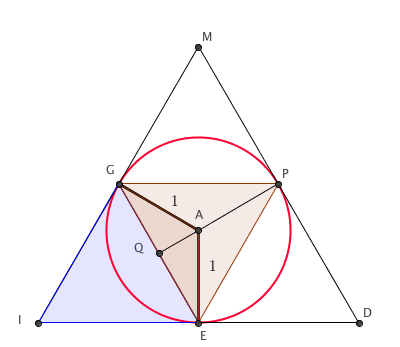
En partant de cette division de la figure, tu peux calculer d'abord dans le triangle rosé, puis ensuite dans le triangle en bleu.
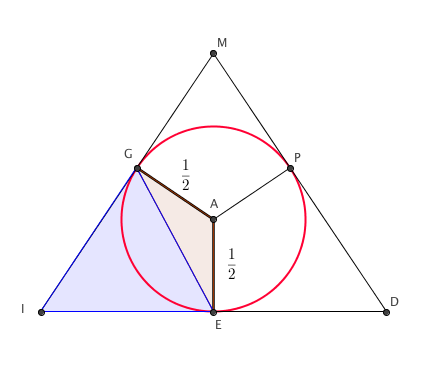
Vous voulez dire tracer au lieu de tirer non ? Je sais que p0 = (3 x 20 x c)/2 (car pn désigne le demi périmètre et c désigne la longueur d'un côté) = 3c/2 et donc c devrait logiquement être égal à 3 ? Je ne vois pas comment procéder autrement et en quoi les 3 rayons perpendiculaires à chacun des côtés pourraient m'aider...
Si j'ai bien compris, le triangle IGE remplace le triangle inscrit dans le cercle de l'énoncé, donc tout ce qu'on dit sur ce triangle s'applique au triangle inscrit et du coup on prouve que p0 = (3racine(3))/2. C'est plutôt malin, j'aurai jamais trouvé, je pensais qu'il fallait se servir du 3x2^n mais ça tombait faux.
Mais du coup que doit on faire pour q0 ? Au début je voulais faire Thalès mais on a pas assez de valeur donc ça marche pas. Je suis bloquée... Help ?
Si j'ai bien compris, le triangle IGE remplace le triangle inscrit dans le cercle de l'énoncé,
Oui, je disais 6 pour le périmètre entier du triangle ^^
Mais du coup en effet ce que l'énoncé veut que l'on prouve ne marche pas :/
J'ai bien fait de m'y prendre à l'avance pour ce dm, d'habitude je le fait la veille de la rentrée mais la il s'annonce bien compliqué !
Bonjour le revoici (enfin ! ) j'ai bien réfléchi et j'ai compris jusqu'à ce que vous dites que cos(AGQ) = cos(/3). Je ne comprend pas car nous avons démontré que AGQ = /6 donc cos(AGQ) devrait être égal à /6 non ?
Ah mais je crois que vous vous êtes trompé car dans l'énoncé il est écrit que le cercle a pour rayon 1 donc AG = 1 et donc GQ = V3/2.
Si on applique cela, je trouve bien comme demi périmètre p0 = (3V3)/2 et q0 = 3V3
Ensuite pour la question b), j'ai trouvé p1 en disant que un hexagone est composé de 3 triangles équilatéraux. Si l'on prend un triangle équilatéral parmi eux, comme le rayon est de 1, tous les côtés dû triangles seront égal à 1 et donc p1 = (6 x 1)/2 = 3.
Après pour q0 je réfléchis mais je ne vois pas l'astuce...
Pour p1 effectivement c'est 3 (3 triangles équilatéraux dont le côté est 1)
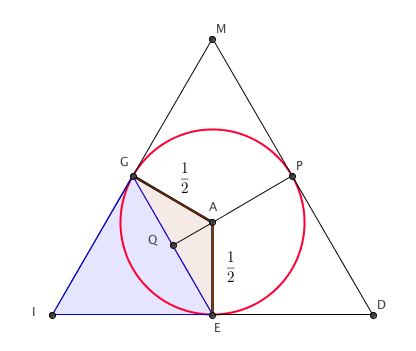
Pour q1 il faut prendre 3 triangles équilatéraux dont la hauteur est 1, et on obtient bien
Après pour la question 2) a) ils me demandent d'exprimer l'angle au centre qui intercepte les côtés de Pn ou de Qn...
Combien y'avait-il de côtés pour n=0, avec quelles valeurs d'angles as-tu travaillé pour le triangle extérieur ? Pour le triangle intérieur ?
Combien y'avait-il de côtés pour n=1, avec quelles valeurs d'angles as-tu travaillé pour le triangle extérieur ? Pour le triangle intérieur ?
Pour n = 0 --> 3 côtés et j'ai travaillé avec une valeur d'angle de 2/3 pour le triangle intérieur et pour le triangle extérieur je ne sais pas ...
Pour n = 1 --> 6 côtés et j'ai travaillé avec une valeur d'angle de /3 pour l'hexagone intérieur et pour l'hexagone extérieur je ne sais pas...
Personne d'autre ne peut m'aider ? Il faut absolument que je finisse ce dm avant demain midi car après je pars et je ne pourrais plus le faire jusqu'à dimanche soir... Quelqu'un pour m'éclairer ?
Je pense qu'il faut reprendre les choses calmement.
Si n=0, on a donc 2 figures (l'une comprise dans le cercle, l'autre à l'extérieur du cercle), chacune ayant côtés.
Dans le triangle AGQ :
Donc :
Avec le triangle GIE :
Annuler
connectez vous