Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques SupérieurOn parle exclusivement de maths, pour le supérieur principalement, les BTS, IUT, prépas... Maths sup ArithmétiqueTopics traitant de arithmétique [tout]Lister tous les topics de mathématiques
Niveau Maths sup
Partager :

Arithmétique dans Z

Posté par
Ayoubgg 22-07-24 à 00:36

Bonjour j'ai besoin d'aide pour répondre à cet exercice merci d'avance.  
Soit n>1
  x_{n} = \frac{(2n)!}{(2\pi)^{2n}} sum_{k=1}^{\infty} \frac{1}{k^{2n}} \]

u_{n} = 2^{n+1} \left( 4^n - 1 \right) x_n \]

v_{n} = sum_{k=1}^{n} 3^{\gcd(k, n)}

Prouvez qu'il existe des entiers positifs a  et b  tels que :

frac{\gcd(v_n, u_n)}{\gcd(a, b)} = n

Posté par
Sylvieg Moderateurre : Arithmétique dans Z 22-07-24 à 07:40

Bonjour,
Peux-tu, en restant dans le même sujet, recopier l'énoncé avec les balises LaTeX nécessaires ?
N'oublie pas d'utiliser le bouton "Aperçu" avant de poster.

Posté par
Ayoubggre : Arithmétique dans Z 22-07-24 à 14:48

soit  n>1 \\ x_n = \frac{(2n)!}{(2\pi)^{2n}} \sum_{k=1}^{\infty} \frac{1}{k^{2n}} \\ \\ u_n = 2^{n+1} \left( 4^n - 1 \right) x_n \\ \\ v_n = \sum_{k=1}^{n} 3^{\gcd(k,n)} \\
Prouvez qu'il existe des entiers positifs a  et b  tels que : \frac{\gcd(v_n, u_n)}{\gcd(a, b)} = n

Posté par
Ayoubggre : Arithmétique dans Z 23-07-24 à 18:13

J'espère que quelqu'un pourra m'aider car je ne sais pas comment répondre à cette question.

Posté par
carpediemre : Arithmétique dans Z 23-07-24 à 19:36

salut

ça m'étonnerait que l'énoncé soit aussi succinct !!

aussi il serait bien de nous donner l'énoncé exact et complet ...

Posté par
Ayoubggre : Arithmétique dans Z 23-07-24 à 19:40

Salut, J'ai écrit l'énoncé de l'exercice en entier, il n'y a pas d'informations supplémentaires.

Posté par
Ayoubggre : Arithmétique dans Z 23-07-24 à 19:43

Cette image représente l'exercice.

Arithmétique dans Z

Posté par
carpediemre : Arithmétique dans Z 23-07-24 à 20:09

et bien dis donc !! parce que ça m'a pas l'air facile

il faudrait déjà :

probablement reconnaitre en x_n à quelle série on a affaire

prouver que u_n est entier

quant à calculer v_n ... ben

alors bon courage et curieux de voir la solution !!

Posté par
Ulmierere : Arithmétique dans Z 23-07-24 à 20:22

Pour v_n, il y a un moyen simple si on se rend compte que pour tout fonction arithmétique f,

\sum_{k=1}^n f(gcd(k,n)) = (f\ast\phi)(n) = \sum_{d | n} f(d)\phi\left(\dfrac{n}{d}\right)

Donc ici, v_n = \sum_{d | n} 3^{n/d}\phi(d)

Posté par
Ayoubggre : Arithmétique dans Z 25-07-24 à 04:38

Pour v_n on a : \sum_{k=1}^{n} 3^{\gcd(k,n)} = \sum_{d \mid n} \sum_{\substack{1 \leq k \leq n \\ \gcd(k,n)=d}} 3^d = \sum_{d \mid n} 3^d \sum_{\substack{1 \leq k \leq n \\ d \mid k \\ \gcd\left(\frac{k}{d}, \frac{n}{d}\right) = 1}} 1 = \sum_{d \mid n} 3^d \sum_{1 \leq r \leq \frac{n}{d}} \gcd\left(r, \frac{n}{d}\right) = 1 = \sum_{d \mid n} 3^d \sum_{1 \leq r \leq \frac{n}{d}} \sum_{s \mid r \mid \frac{n}{d}} \mu(s) \\ \\ \\ \\ = \sum_{d \mid n} 3^d \sum_{1 \leq r \leq \frac{n}{d}} \sum_{\substack{s \mid r \\ s \mid \frac{n}{d}}} \mu(s) = \sum_{d \mid n} 3^d \sum_{s \mid \frac{n}{d}} \mu(s) \sum_{\substack{1 \leq r \leq \frac{n}{d} \\ s \mid r}} 1 = \sum_{d \mid n} 3^d \sum_{s \mid \frac{n}{d}} \mu(s) \frac{n}{ds} \\ \\ \\ \\ = \left(\sum_{ds \mid n} \frac{3^d \mu(s)}{d s}\right) n.
Mais j'ai encore du mal à identifier a et b.

Posté par
Ulmierere : Arithmétique dans Z 25-07-24 à 14:05

A mon avis, ça ne te mènera pas bien loin car il n'y a rien qui montre dans ton calcul que tous les 3^d\mu(s)/(ds) soient des entiers

Posté par
GBZMre : Arithmétique dans Z 28-07-24 à 10:04

Bonjour,
L'énoncé me semble chelou, avec ces a et b. Il y a aussi une imprécision sur l'ordre des quatifications. Est-ce que l'on ne demande pas simplement de montrer que n divise u_n et v_n ?

Posté par
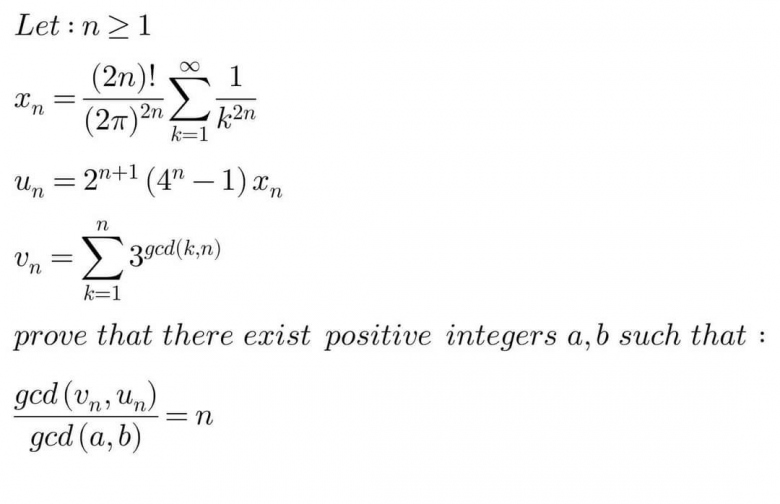
Ayoubggre : Arithmétique dans Z 31-07-24 à 02:31

Bonjour, Oui, après avoir essayé de résoudre l'exercice, je me suis demandé Pourquoi utiliser $\gcd(a,b)$ au lieu de simplement un entier positif c


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1717 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !