Inscription / Connexion Nouveau Sujet
Asymptote oblique
Bonsoir a tous,
J'ai un exercice de math a finir et je bloque a une question,
Donc déjà voici l’énonce :
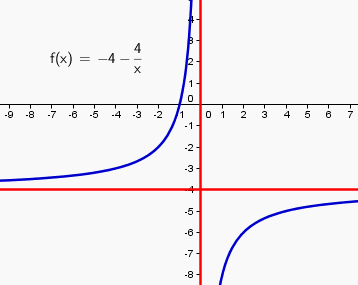
Soit f: (]0,+infini[->R
x|->-4-4/x
J'ai déterminer les limites de f aux bornes de son ensembles de définition
Lim f(x)= - infini
x|->0
Lim f(c) = - infini
x|-> +infini
Voici la question ou je bloque :
Montrer que la courbe représentative C de f admet deux asymptotes ont une oblique.
Donc déjà je crois avoir trouvé la première asymptote : Asymptote verticale d’équation x=0 dites moi si je me trompe.
Mais pour l’asymptote oblique je n'y arrive pas, en plus je dois etudier la position de C par rapport a l'asymptote oblique mais je ne la trouve pas
Donc si on pouvait m'aider, Thanx
Voila c'est fait : lim f(x)+x = -x-4/x+x =0
x|-> +infini
je trouve bien zéro donc la courbe C admet bien une asymptote oblique mais comment étudier sa position par rapport a C ? vu que je ne connais rien sur l'asymptote oblique, je sais juste quelle existe.
Encore Merci
l'équation de cette asymptote c'est y = -x puisque quand x 
, la distance entre la courbe (f(x)) et la droite (y = -x) 0
la position par rapport à l'asymptote est donnée par le signe de f(x) - (-x)
Ok donc y= -x
y= -infini
ok maintenant que j'ai trouver sa que veut dire la phrase suivante :' etudier la position de C par rapport a l'asymptote oblique'
Ok donc y= -x
y= -infini
(indépendemment qu'on ne peut pas écrire "y = -
"
soit c'est "limite de y quand x
= -"
(
soit c'est "quand x
+, y ")
soit y = ax+b une asymptote (oblique)
f(x) une courbe quelconque
la droite y = ax+b est asymptote oblique de f(x) si et seulement si la distance entre les deux c'est à dire f(x) - (ax+b) tend vers 0
quand x
Ici l'asymptote a pour équation y = -x
et f(x) - (-x) = -x-4/x+x = -4/x
et tu as bien dit correctement dans ton post de 22h29 que la limite quand x
était 0 . OK
alors que veut dire ce post de 22h39 avec cette phrase qui vient comme un cheveu sur la soupe ???
"etudier la position de C par rapport a l'asymptote oblique"
j'ai déja répondu :
la position par rapport à l'asymptote est donnée par le signe de f(x) - (-x)
la position de f(x) par rapport à son asymptote oblique y = ax+b est donnée par le signe de f(x) - (ax+b)
si f(x) - (ax+b) > 0, c'est à dire f(x) > (ax+b) la courbe est "au dessus" de son asymptote
si f(x) - (ax+b) < 0, c'est à dire f(x) < (ax+b) la courbe est "au dessous" de son asymptote
ici c'est donc le signe de f(x) - (-x) = -4/x qui dit si la courbe est au dessus ou au dessous de son asymptote
Annuler
connectez vous