Inscription / Connexion Nouveau Sujet
Asymptotes
Bonjour j'ai besoin de votre aide svp
Exercice :
Dans chacun des cas suivants , déterminer les asymptotes à la courbe représentative (C) de la fonction f.
Réponses :
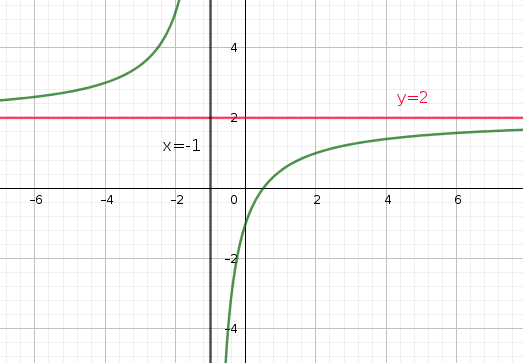
donc la droite d'équation y=2 est asymptote à la courbe (C) en
La droite d'équation x=-1 est asymptote à (C)
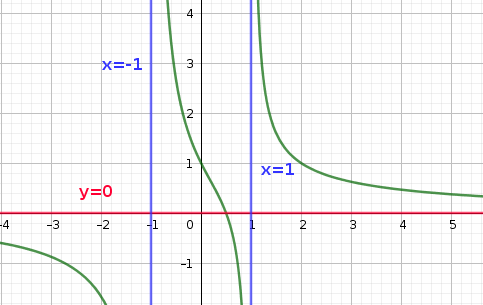
La droite (OI) est asymptote à la courbe (C) en
La droite d'équation x=-1 est asymptote à la courbe (C)
La droite d'équation x=1 est asymptote à (C)
Bonjour
as-tu eu l'idée de tracer tes représentations graphiques avec geogebra par exemple pour te vérifier ?
il faudrait distinguer les cas vous avez fait un copier-coller pas partout
a) deux asymptotes y= 2 et x=-1
b) 3 asymptotes
Bonjour
as-tu eu l'idée de tracer tes représentations graphiques avec geogebra par exemple pour te vérifier ?
Non! , je ne sais pas comment voir les asymptotes ( je sais juste les tracer)
Vous redémontrez ce que vous avez déjà écrit
asymptote parallèle à l'axe des abscisses
à l'axe des ordonnées non définie en un point et limite infinie quand x tend vers ce point
non parallèle aux axes limite infinie, limite de
et
donc la droite y=2 est asymptote à(C) en
La droite d'équation x=-1 est asymptote à (C)
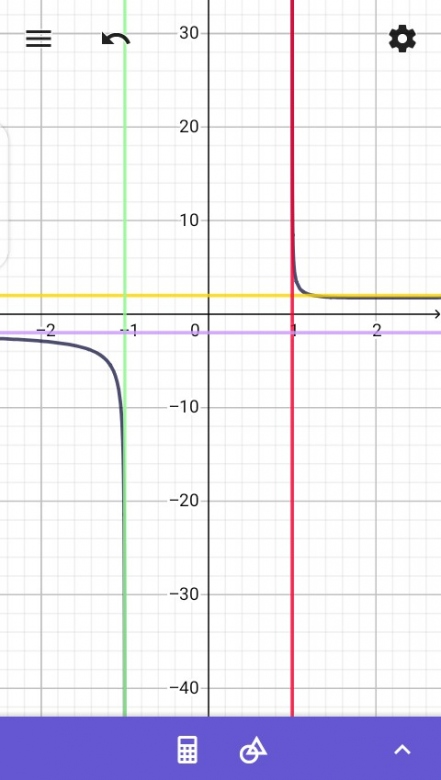
La droite d'équation x=1 est asymptote à (C)
La droite d'équation y=2 est asymptote à (C)
D'accord
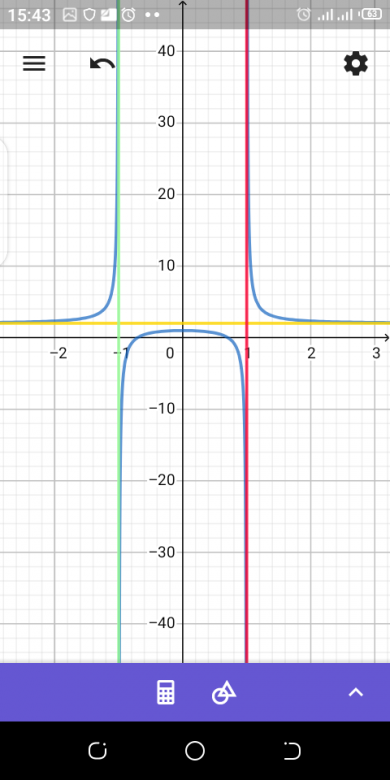
Les droites d'équations y=2 et y=-2 sont asymptotes à (C) respectivement en
Les droites d'équations x=-1 et x=1 sont asymptotes à (C)
Samsco, ne mets pas d'étoile en début de ligne, cela fait plusieurs fois que je les enlève, car le Ltx semble perturbé et l'affichage était mauvais 
salut
il est toujours dangereux d'écrire une suite d'égalité de limite sans rien vérifier ... en particulier lorsque l'une d'entre elles contient une forme indéterminée comme ici par exemple :
la deuxième cumulant d'ailleurs deux FI : oo/(oo - oo)
pour calculer les limites de f à l'infini, en -1 et en 1 j'écris f(x)sous les trois expression suivantes :
la première expression me donne de plus l'asymptote immédiatement ...
pour les deux dernières je calcule/donne la limite de chaque facteur et je conclus par produit ...
d'autre part on peut noter que f est paire donc il suffit de calculer les limites en +oo et en 1 pour avoir celle en -oo et en -1 ...

Samsco, ne mets pas d'étoile en début de ligne, cela fait plusieurs fois que je les enlève, car le Ltx semble perturbé et l'affichage était mauvais

Ah je savais ,je ne savais!
carpediem
Je suis allé allé un peu vite parce que l'exercice est long à faire , si j'écrivais tout dans les détails , avec Ltx , ce serait encore plus long.
pas du tout !!! mauvaise excuse !!!
on mets autant de temps sinon moins à écrire proprement (= mathématiquement) les choses et même avec latex ou un peu de latex ...
c'est long parce que tu écris des égalités de limites (qui sont donc fausses (FI) ou inutiles)
il suffit d'écrire des égalités d'expressions et de ne calculer qu'une limite à la fin !!!
pas du tout !!! mauvaise excuse !!!
on mets autant de temps sinon moins à écrire proprement (= mathématiquement) les choses et même avec latex ou un peu de latex ...
c'est long parce que tu écris des égalités de limites (qui sont donc fausses (FI) ou inutiles)
Même sans les égalités de limite , ça reste long.