Zut j'ai loupé ton message.

Non en fait je ne suis pas lycéenne et l'ai été il y a plusieurs années... en filière littéraire.

Donc là le bac S c'est toute seule, d'où le fait que je n'ai pas forcément les données de manière linéaires comme si j'avais des cours, et que je jongle un peu entre première et terminale!

Hum, littéraire ça ne se voit pas, désolée pour les fautes, j'ai la fâcheuse manie de me relire après avoir posté dans l'optique d'éditer, ce qui n'est pas possible ici.

alors attention il y a une chose qui t'échappe :

pour la fonction choisie en exemple
f : x -> x²
tu as montré que pour l'abscisse a, le coefficient directeur est 2a
pour l'abscisse b, ce coefficient sera 2b
pour l'abscisse 4,5, ce coefficient sera 2*4,5=9

pour l'abscisse quelconque x, ce coefficient sera 2x
selon ton expression : pour chaque point d'abscisse x, on "fait" 2x, pas 2a.x, car alors 'a' n'a de définition que si tu parles de l'abscisse 'a', si tu parles de l'abscisse 'x', 'a' n'a plus d'existence.

c'est pour cela qu'on définit la fonction dérivée f' de la fonction f
f' x: -> 2x

et pur les fautes, que j'ai l'habitude de corriger, ne t'inquiète pas : tu es largement au-dessus du lot.
par exemple, l'utilisation correcte des à ô et autres ç me ravit.

Ok, c'était ce que j'avais compris au premier abord, mais après avec ta formule comme je trouvais 2ax (je me suis peut-être plantée dans le calcul?) je ne savais plus...

Merci infiniment pour toutes tes explications, ça m'aide vraiment beaucoup!

Pour quelqu'un qui a fait L, les erreurs que j'ai faites au-dessus ne sont pas top quand même! Je suis supposée ne pas en commettre.

Sinon pour les "à", "ç" etc... c'est quand même la base

Ton français est loin d'être approximatif, et on sent bien que ta "pensée" est structurée, si je peux me permettre.

si on a fait L on écrit  alors  " or " et pas hors  ( voir le message au début )

Effectivement il y en a de "jolies" fautes, et mon "hors" en fait partie. Merci.

de rien, ne le prenez pas mal mon intervention diplomatique et néanmoins active ....Les gens ne savent plus écrire correctement il faut se relire ( ça m'arrive aussi parfois )

C'est un peu tard pour ne pas le prendre mal

Je disais justement de moi-même que je faisais des fautes que je ne devais pas commettre, alors forcément, une intervention aussi tranchante par la suite c'est plutôt blessant et rabaissant.

Cela dit je suis également pour l'utilisation correcte du français, et d'avis aussi qu'il faut se relire même si, comme je le disais, j'ai pris la mauvaise habitude de le faire après avoir envoyé mes messages, ce qui crée de mauvaises surprises sur les forums où ceux-ci ne peuvent pas être modifiés.

Bref, votre intervention est tout à fait justifiée et je l'accepte!

TB  mon moral remonte au zénith de ma jovialité et ce n'est pas peu dire. Ne l'ébruitez surtout pas trop .

Bonjour!

Encore une petite question pour savoir si j'interprète bien une leçon sur Maxicours...

Si on me demande si une fonction est dérivable en x₀ et que je suis obligée de regarder à droite et à gauche, donc si x₀=1 en 1⁺ et en 1^-, et que les deux résultats sont identiques, c'est que la fonction est bien dérivable en x₀? Par contre si j'ai deux résultats différents c'est qu'elle ne l'est pas?

Merci!

exactement

le coup classique est avec les valeurs absolues :
f(x)=|2x-1|

elle est dérivable à gauche de 1 et le nombre dérivé est -2
elle est dérivable à droite de 1 et le nombre dérivé est +2

les deux étant différents, elle n'est pas dérivable en 1

bien sur, l'exemple semble un peu artificiel.
il est là uniquement pour illustrer le cas d'école.

Je te remercie beaucoup pour ta réponse super rapide! Ca commence à bien s'éclaircir dans ma têtes et sur mes fiches

Ahhhh en fait ce n'est pas si clair, je n'arrive pas à obtenir comme toi!

J'obtiens 2 dans tous les cas:

(f(1^-+h)-f(1^-))/h

(2(1^-+h)-1)-(2^--1))/h

(2^-+2h-1-2^-+1)/h

2h/h

et donc j'ai 2, je présume qu'il y a quelque chose que je n'ai pas saisi avec les valeurs absolues... Je pensais qu'une fois qu'on avait calculé le résultat de (2x-1), s'il était négatif on devait retirer le "-" et que ça donnait bien f(x) mais à priori ça doit être plus complet que ça!

j'ai fait une erreur dans mon message précédent, il s'agit d'étudier la dérivabilité au voisinage de 1/2, pas de 1

soit la fonction suivante :
f(x)=|2x-1|

f(-5)=|-10-1|=|-11|=11
f(5)=|10-1|=|9|=9

si 2x-1 est négatif, alors f(x)=|2x-1|=-(2x-1)=1-2x
si 2x-1 est positif, alors f(x)=|2x-1|=+(2x-1)=2x-1

le taux de variation au voisinage de 1/2 est
on pose x=1/2+h, donc 2x-1=2h
le taux de variation vaut

pour x<1/2, il faut voir que 2x-1=2h<0, h<0, donc |h|=-h
le taux de variation vaut alors
sa limite quand x tend vers 1/2, en restant < 1/2 est -2

pour x>1/2, il faut voir que 2x-1=2h>0, h>0, donc |2h|=+2h
le taux de variation vaut alors
sa limite quand x tend vers 1/2, en restant > 1/2 est +2

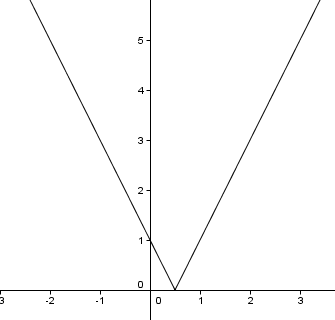
sur le graphique, le graphe est une demie-droite décroissante pour x<1/2 (de pente -2, donc négative), une autre demie-droite croissante pour x>1/2 (de pente +2, donc positive)

au voisinage de 1, la fonction est dérivable à gauche de 1 et vaut 2, à droite de 1 et vaut aussi 2, donc au voisinage de 1, elle est dérivable.

Merci beaucoup pour tes explications toujours très complètes.

Il y a une toute petite chose (mais qui change tout) que je ne comprends pas:

Tu écris |h|=-h : une valeur absolue n'est-elle pas forcément positive? J'aurais compris |-h|=h mais l'inverse j'ai du mal, je pense que je passe à côté d'une notion importante.

si h=-2 par exemple
|h|=2=-h

le signe '-' indique l'opposé d'un nombre, pas un nombre négatif

si le nombre h est lui-même négatif, son opposé -h est positif

donc on retient :

dans tous les cas : |-h|=|h|

si h est positif : |-h|=|h| = h

si h est négatif : |-h|=|h| = - h

Ahhh oui je n'avais pas pensé au fait que h désignant un nombre négatif, -h était donc positif!

Merci bien pour la précision!