Inscription / Connexion Nouveau Sujet
Avec et sans repère
Bonjour pouvez-vous m'aider pour cet exercice s'il vous plait.
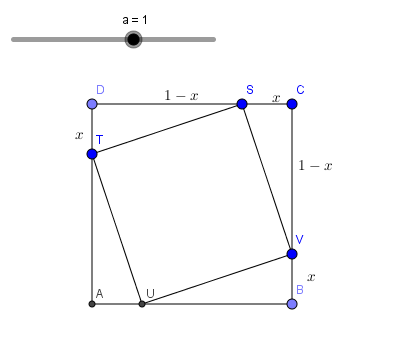
Soit ABCD un carré.Les points U,V,S etT appartiennent aux côtés (AB), (BC), (CD)et (DA)et AU=BV=CS=DT.
1)Justifier que (A,B,D) est repère orthornomé.
2)on suppose dans cette question que AU=1/4 AB.
Lire les coordonnée de U,V,S et T puis démontrer que UVST est un carré.
3)Reprendre la question 2 avec U quelconque sur (AB).
On note x l'abscisse de U.
4)Démontrer que UVST est un carré sans utiliser de coordonnées.
Pour la question 1,je vois comment démontrer que (A,B,D) est repère orthornomé.
Merci d'avance.
Bonjour, voilà ce que j'ai fait.
1)DB²=AB²+AD²
DB=√(0-1)²+(1-0)²
=√1+1=√2
AB=√(0-1)²+(0-0)²
=√1+0=√1
AD=√(0-0)²+(0-1)²
=√0+1=√1
√1+√1=√2
pourquoi calculez-vous des distances?
vous avez un carré donc (AB) et (AD) sont perpendiculaires
vous avez aussi AB=AD=1 c'est un losange
d'où repère orthonormé
Ha oui, je me suis trompé.Si j'écrit que le repère (A, B, D) est un repère orthonormé car il est défini par 3 points A,B,D formant un triangle rectangle isocèle de sommet A.
AD=AB et AD est perpendiculaire à AB.
Donc c'est bon .J'ai réflechi pour la question 2 mais le problème c'est que les diogonales n'ont pas les même milieu.Pourtant il affirme que c'est un carré.Pouvez-vous vérifier mon calculs.
U (1/4;0),V (1;1/4),S (3/4;1),T (0;3/4)
Soit A milieu (VS)
Xa=XS+XV/2=1+0,75/2=1,75/2=0,875
YA=YS+YV/2=0,25+1/2=1,25/2=0,625
Donc A (0,875;0,625)ou(7/8;5/8)
Soit B milieu (UT)
XB=XU+XT/2=0,25+0/2=0,125
YB=YU+YT/2=0+0,75/2=0,375
Donc B (0,125;0,375)ou (1/8;3/8)
il faut garder une figure sous les yeux
vous auriez vu que vous avez calculé les coordonnées du milieu de 2 côtés opposés
les diagonales sont [TS] et [SU] et I
attention à l'écriture en ligne il manque des parenthèses
évitez aussi les homonymies A et B étaient déjà définis
Je comprend pourquoi mes calculs étaient faux.
TV=XT+XV=(0+1)/2=0,5
=YT+YS=(0,75+0,25)/2=0,5
Les coordonnée du milieu de TV sont (0,5;0,5)
SU=XS+XU=(0,75+0,25)/2=0,5
=YS+YU=(0+1)/2=0,5
Les coordonnée du milieu de SU sont (0,5;0,5)
Donc les diagonales (TV)et (SU) ont le même milieu.Donc UVST est un parrallélogramme.
Aprés il faut donc que je démontre que UVST est un losange .
SV=√(XS-XV)²+(YS-YV)²
=√(0.75+1)²+(1,+0,25)²
=√(3,0625 +1,5625)=√4,625
ST=√(XV-XS)²+(YV-YS)²
=√(0,75+1)²+(0+0,75)²
=√(3,0625+0,5625)=√3,625
Le problème c'est que SV n'est pas égale à ST.J'ai essayé tout les combinaisons pourtant.
pourquoi ne pas garder les fractions et pourquoi certains se transforment-ils en
" alt="+
 " class="tex" />
" class="tex" />
c'est un losange
Merci de me le faire remarque ,j'ai mis un +au lieu - .Si vous n'étiez pas là ,j'aurais raté l'exercice à cause d'une petite erreur.Puis après,j'ai fait ça.
TV=√(0-1)²+(3/4-1/4)²
=√(1+1/4)
=√5/4
TV²=5/4,
ST²=(10/16)
SV²=(10/16)
TV²=ST²+SV² donc d'aprés la réciproque du théoréme de pythagore:le triangle TVS est rectangle en V.
Oui
vous pouvez simplifier
comme j'ai écrit plus haut
conclusion c'est un carré
Vous refaites exactement la même chose avec x au lieu d'un quart.
Il y aura des simplifications en moins.
Que proposez-vous pour la question 4 ?
les quatre triangles sont isométriques
même valeur de l'angle compris entre deux côtés de même mesure
donc UV=VS=ST=TU
on en déduit parallélogramme ou directement losange
puis les diagonales sont de même mesure donc rectangle
Je vous remercie infiniment pour votre aide.Grâce à vous, je saurais refaire un exercice similaire .


