Bonjour à tou(te)s,
J'ai un DM à faire pour mercredi, j'ai un peu de difficultés, voici l'énoncé :

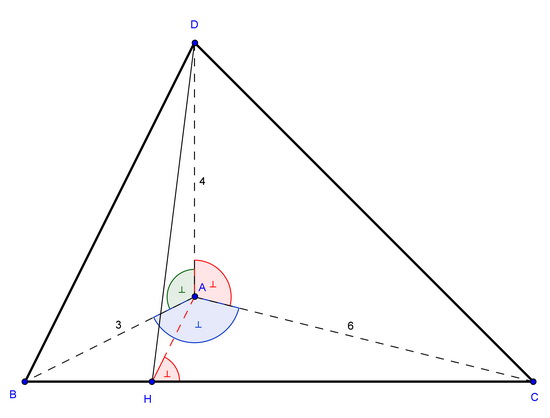
Le tétraèdre ABCD a trois de ses faces qui sont des triangles rectangles : DAC, BAD, CAB sont rectangles en A. Et soit AH la hauteur du triangle ABC.

On sait également que AB=3 cm, AD = 4 cm et AC = 6 cm

1°) Quel est le volume de ce tétraèdre ?

2°) a) Calculer BC et en déduire sin (ABC)
b) H étant la hauteur issue de A dans ABC, déduire de la question 2a) la distance AH puis calculer CH.
c) Justifier la nature du triangle DAH et calculer DH.
d) Montrer que HDC est un triangle rectangle en H.
e) Calculer l'aire du triangle BDC

3°) Déduire de 1 et de 2e) la longueur de la hauteur issue de A du tétraèdre.

Pour la question 1)
J'ai trouvé V= 1/3 x B x h = 613, est-ce que c'est bon ?

2a) Pour BC, je trouve avec l'application du théorème de Pythagore dans le triangle ABC rectangle en A : BC=35