Inscription / Connexion Nouveau Sujet
Axes de rotation et angle à partir d'une matrice de rotation
Bonjour,
Après avoir fait quelques recherches j'ai trouvé un formule toute faite qui permet de passer d'une matrice de rotation 3x3 à un axe de rotation et son angle.
angle = acos(( m00 + m11 + m22 - 1)/2)
x = (m21 - m12)/?((m21 - m12)2+(m02 - m20)2+(m10 - m01)2)
y = (m02 - m20)/?((m21 - m12)2+(m02 - m20)2+(m10 - m01)2)
z = (m10 - m01)/?((m21 - m12)2+(m02 - m20)2+(m10 - m01)2)
Cependant, la personne n'a pas mis de démonstration et j'aimerais comprendre comment il a trouvé ceci.
Pouvez vous me donner des pistes ou des explications ?
Au passage me dire si ces résultats sont justes ?
Merci
Voici un lien 
intéressant mais en anglais.
Il y a une différence au niveau de la formule de calcul de l'angle à un facteur 2 près.
Bonjour,
@Razes :
Merci du lien.
Après avoir fait d'autres recherches j'ai vu qu'une matrice de rotation pouvait s'écrire de la forme suivante avec c=cos(angle), s=sin(angle) et u un vecteur unitaire (cf image attachée tout en bas)
Y-a-t'il un nom à ce théorème ?
A partir de ça je peux trouver facilement les valeurs de ux uy et uz.
@verdurin :
Par contre pour l'angle je ne vois pas trop.
La trace restant invariante par changement de base, j'imagine donc qu'il existe une base dans laquelle je peux écrire ma matrice avec des cosinus sur la diagonale ... par contre le -1 me gêne.
Sinon sur le lien qu'a donné Razes , il est marqué plusieurs fois que l'angle vaut acos(( m00 + m11 + m22 - 1)/2).
Je ne peux pas savoir s'il y a un facteur 2 pour le moment étant donné que je ne sais pas comment trouver l'angle.
Un peu d'aide svp ?
Soyons sérieux. Comme l'a dit verdurin, la détermination de l'angle (géométrique) d'une rotation vient du fait que la trace ne dépend pas de la base dans laquelle on écrit la matrice. Or, dans une bon bien choisie, la matrice d'une rotation d'angle géométrique s'écrit
et donc la trace de la matrice de rotation (dans n'importe quelle base) est toujours .
L'axe d'une rotation qui n'est pas l'identité est la droite propre associée à la valeur propre 1.
Remarquons qu'une rotation n'est pas entièrement déterminée par son axe et son angle géométrique : en effet on ne sait pas si l'on doit tourner de
dans un sens ou dans l'autre !
La rotation n'est entièrement déterminée que par son axe et l'angle orienté de rotation dans un plan orthogonal à l'axe.
Merci beaucoup de vos réponses.
C'était simple en fin de compte, il me manquait juste quelques connaissances mathématiques.
Problème résolu
@Recomic35
Je pense que tout le monde est sérieux et a essayé de répondre à la question:
Après avoir fait quelques recherches j'ai trouvé un formule toute faite qui permet de passer d'une matrice de rotation 3x3 à un axe de rotation et son angle.
angle = acos(( m00 + m11 + m22 - 1)/2)
x = (m21 - m12)/?((m21 - m12)2+(m02 - m20)2+(m10 - m01)2)
y = (m02 - m20)/?((m21 - m12)2+(m02 - m20)2+(m10 - m01)2)
z = (m10 - m01)/?((m21 - m12)2+(m02 - m20)2+(m10 - m01)2)
Bien entendu, à partir d'une matrice donnée 3x3, on cherche le vecteur normé invariant de la transformation, on cherche un vecteur normé perpendiculaire puis on complète notre base orthonormée par un troisième vecteur normé. Ainsi nous constituons notre matrice. Mais ce n'est pas la réponse à question posée par LePetitPois.
Je maintiens, le lien donné par Razes n'est pas très sérieux d'un point de vue mathématique.
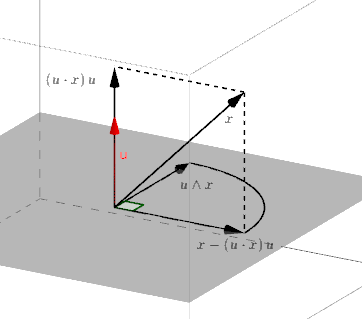
Pour ce qui est de la matrice écrite par LePetitPois, elle vient immédiatement de l'écriture vectorielle de la rotation r d'axe dirigé et orienté par le vecteur unitaire u et d'angle orienté de mesure \alpha :
Je maintiens, le lien donné par Razes n'est pas très sérieux d'un point de vue mathématique.
Ah bon, sincèrement je suis désolé que ce site ne soit pas sérieux mais pourrez vous nous dire pourquoi?
Concernant ce qu'a dit verdurin, personne ne l'a contredit, et voici la preuve:
Pour ce qui est du dessin, c'est la transcription de ce que j'ai écrit:
Bien entendu, à partir d'une matrice donnée 3x3, on cherche le vecteur normé invariant de la transformation, on cherche un vecteur normé perpendiculaire puis on complète notre base orthonormée par un troisième vecteur normé. Ainsi nous constituons notre matrice. Mais ce n'est pas la réponse à question posée par LePetitPois.
Annuler
connectez vous
géométrie en post-bac