Inscription / Connexion Nouveau Sujet
Bac ES Liban 2006
Bonjour,
je viens de faire le 1er exercice des annales Liban 2006,
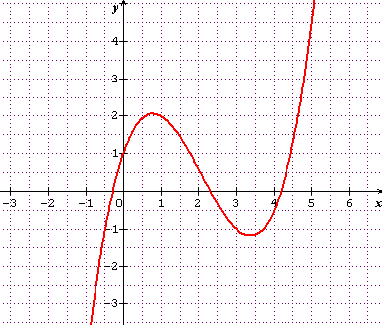
On donne cette représentation graphique :
Donc on calcule assez facilement f(0) = 1 et f(1) = 0
f '(0) = 3 et f '(1) = 0
Ensuite on nous dit que g(x) = ef(x)
On calcule les limites, le tableau de variation de g(x) sans problèmes.
Ensuite, on nous demande g'(0) et g'(1).
En appliquant la formule de la dérivée de e^u on trouve :
g'(0) = f '(0)*e^(f(0)) = 3*e
g '(1) = f '(1)*e^(f(1)) = 0
C'est la première fois que je croise ce genre d'exo. Une fois qu'on a compris, c'est assez simple, mais il faut avoir le réflexe de se servir de la formule.
Qu'en pensent les élèves de ES ?
J'ai lu : est-ce que f(0)=1 ou 2 
Et comme l'axe des ordonnées n'est pas normé, je pensais que c'était ta question...
Kévin pourrait nous chercher l'équation en x^3 de la courbe bleue avec les contions données
et faire une courbe rouge exp(f(x))...

Les questions, c'est pour les élèves qui passent le bac ES. Cette question m'a franchement desarçonnée, alors qu'en fait, c'est assez facile. J'ai même cru qu'il y avait une formule que j'ignorais, alors que c'est la formule générale de e^u
en effet, borneo, la fonction en x^3 sera une régression polynomiale de degré 3 et n'est juste pour tenter d'avoir une représentation pas trop fausse de g(x)
:=
Oui, qu'ils me disent s'ils trouvent ça dur ou non.
Désolée que tu aies perdu un point sur mon topic 
plus serieux , en S , c est pas trop dur !! en ES peut-etre ne sont-ils pas habitués a ce genre d ex
Demain, je fais Pondichery 2005 
Spmtb, toi qui es prof, tu n'as pas l'impression que les bacs exotiques sont plus durs que ceux de métropole ?
J'ai l'impression que les interprétations graphiques ne sont rencontrées que le jour du bac. Un peu tard...
Très joli Kévin 
Comment tu as fait ?
Mais ma courbe d'origine avait une asymptote verticale en -1 et une asymptote oblique. Ne me dis pas qu'avec du x^3 on y arrive... 
J'ai pris 3 points de la courbe et j'ai résolu un système 
Mais sinon ce n'est pas la même courbe, ici pas d'asymptote, il suffit de calculer f(x)/x pour s'en rendre compte.
C'était juste pour avoir la même allure de courbe.

Une question : on peut toujours trouver une équation pour coller à une courbe, ou dans certains cas, c'est impossible ? Je suppose qu'on pourrait améliorer la précision, mais y a-t-il une limite au-dela de laquelle on ne peut plus ?
borneo > Si on a une fonction continue on pourra toujours l'approcher par un polynôme (interpolation avec Lagrange), ou dans certains cas si on reconnait une croissante exponentielle ou d'autres trucs on arrive se débrouiller, maintenant pour trouver l'équation exacte c'est pas toujours possible. Mais oui ici on pourrait encore améliorer la précision.

Je ne parle pas forcément de celle-là. Je me demandais si les maths sont assez fortes pour décrire parfaitement le réel...
Kévin si on a une fonction continue,on pourra l'approcher aussi près que l'on veut par des polynomes(en utilisant les polynomes de Bernstein par exemple) ou des fractions rationnelles.
Après c'est quoi le problème exactement on te donne une courbe,et il faut trouver l'équation qui s'en rapproche le plus?
Bien en augmentant le nombre de points c'est sur que t'auras quelque chose de plus en plus précis.
Voila le renfort 
Bon on est d'accord pour approcher une courbe en étant de plus en plus précis. Mais est-ce que l'on peut trouver l'équation exacte de n'importe quelle courbe ? C'est ça la question de borneo.
Exacte non je pense pas vu que déja si tu testes des polynomes ca sera surement pas exact et même si la limite à l'infini de polynomes de degré de plus en plus grand ca te donne une série entière mais toutes les fonctions ne s'écrivent pas comme ca.
bonjour à tous
je m'immisce
quand j'ai proposé à Kévin de chercher à interpoler f par un P3(x) c'était uniquement, comme je l'ai dit à 20:37, à tenter de "voir" g(x) à l'infini
Ainsi, c'était pour "voir" qqchose du type :
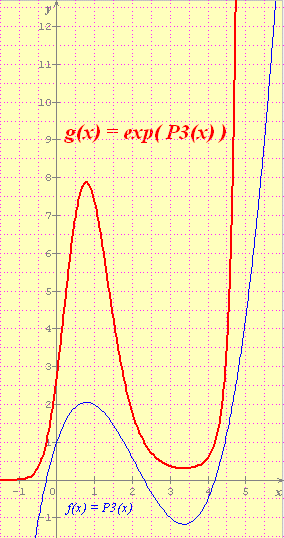
et non pour "décrire le réel" comme le supposais borneo

Merci Mikayaou. En fait, la discussion qui a suivi cherchait à voir si les maths peuvent décrire parfaitement le réel 
J'ai une autre question sur un sujet de bac. Je devrais ouvrir un nouveau topic, mais je ne voudrais pas faire voir à tout le monde que je sèche sur des sujets de bac ES 
Dans un vrai-faux, on demande si x*2^(x-1) est la dérivée de 2^x
Intuitivement, je dirais non, je ne vois pas pourquoi. Mais j'ignore la formule qui permet de dériver 2^x et je ne vois pas où la chercher...