Inscription / Connexion Nouveau Sujet
barycentre
Bonjour
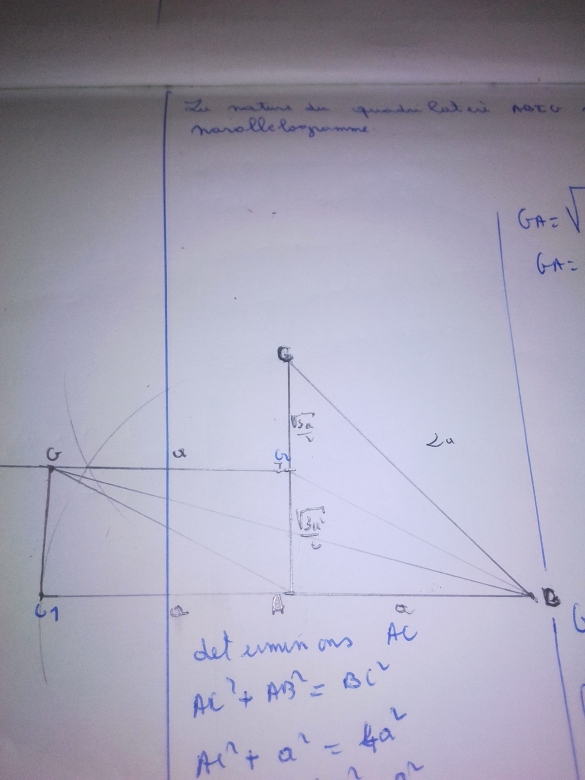
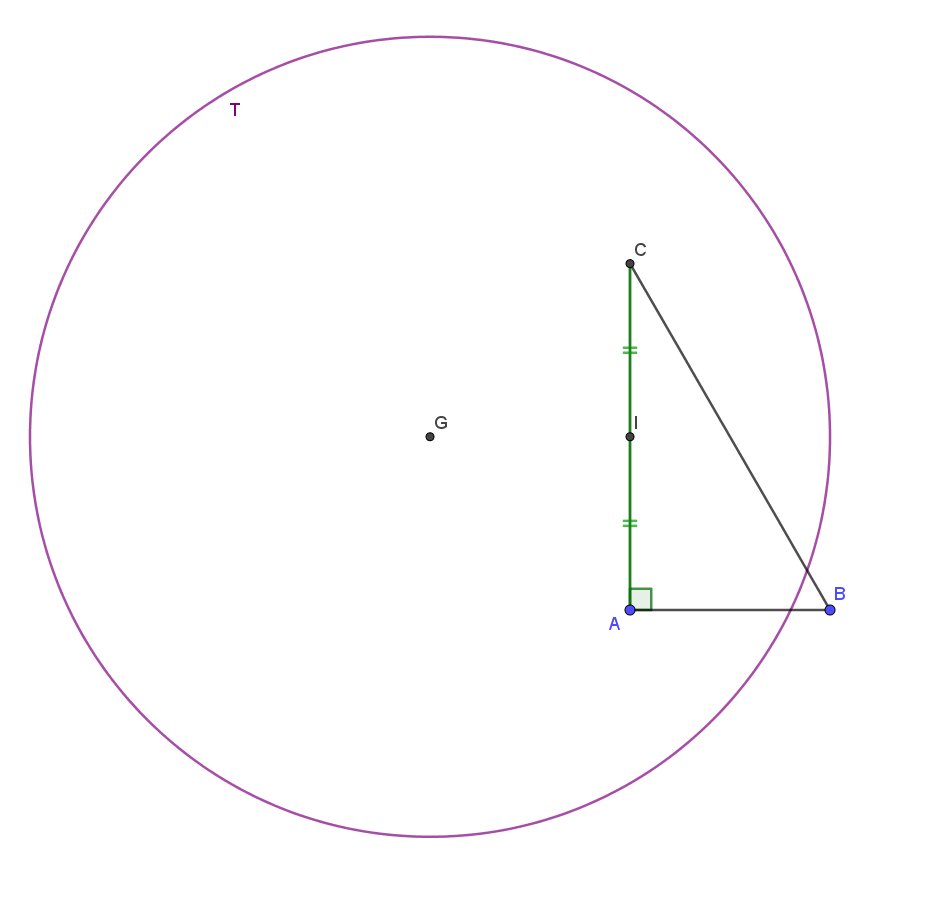
ABC est un triangle rectangle en A tel que AB=a et BC=2a . I désigné le milieu de [ AC] et G le barycentre du système (A, 3)( B, -2) (C,1)
1/ construire le point G et préciser la nature du quadrilatère ABIG
Exprimer en fonction de a les distances GA, GB et GC
2/ a tout M du plan on associe le nombre réel f(M)=3MA-2MB^2+MC.
a/ Exprimer f(M) en fonction de MG et a
a/ déterminer et construire l ensemble (T) des points M du plan tels que f(M)=2a^2
3/ A tout point M du plan , on associe maintenant le nombre réel
h(M)=3MA^2-2MB^2-MC^2
a/ démontrer qu il existe un vecteur U non nul tel que h(M)=VecteurMB.vecteur U-2a^2
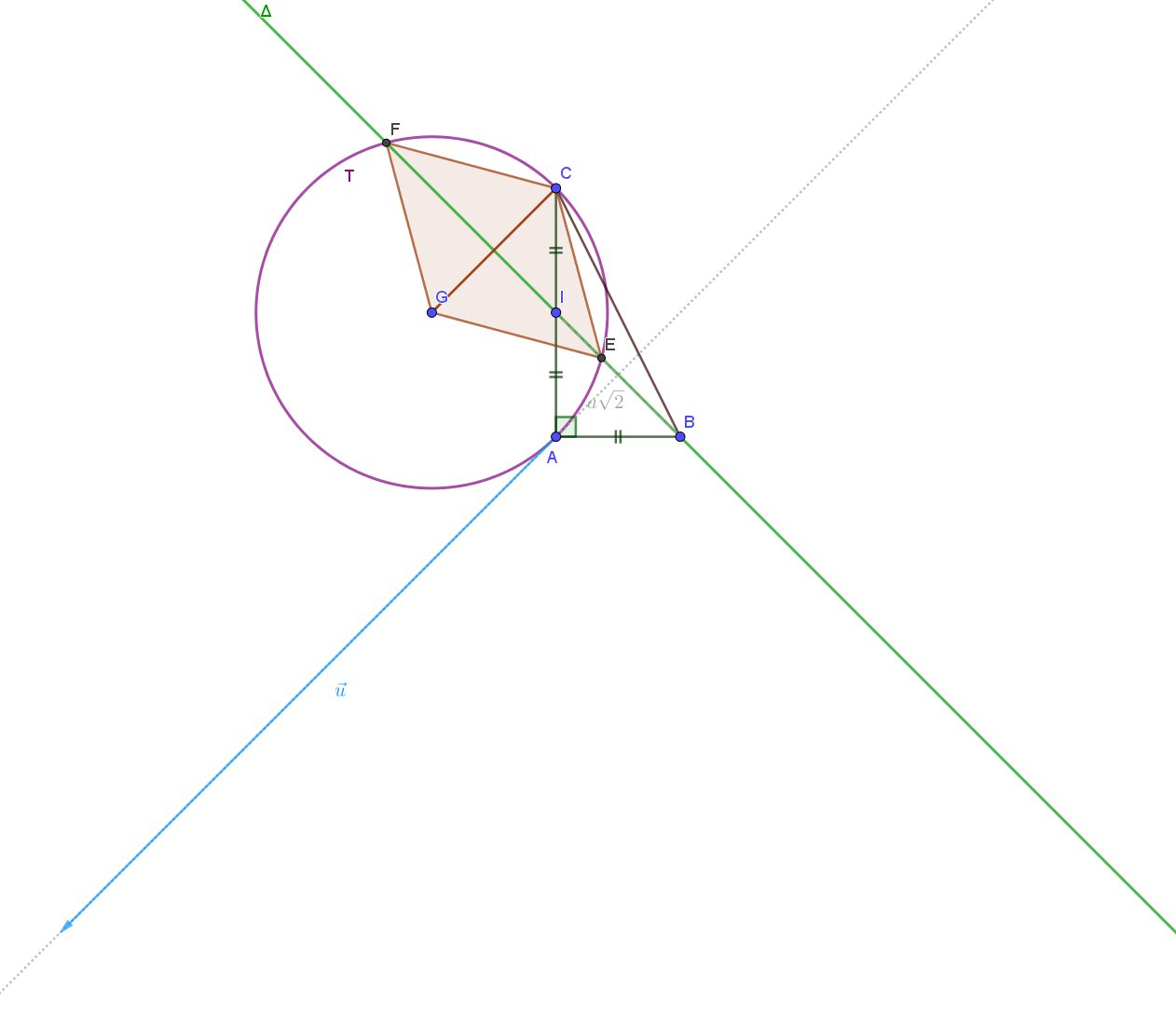
b on désigné par (∆) l ensemble des points m du plan tels h(M) =-2a^2
Vérifier que les points I et B appartient a (∆) . préciser la nature de cet ensemble.
Construire (∆)
4/ (∆) et (T) sont sécantes en deux points E et F. Montrer que les triangles GEC et GFC sont équilatéraux
Reponse
1/ voir la figure ci dessous
La nature du quadrilatère est un parallélogramme.
Question 2
Déterminons AC
AC^2+AB^2=BC^2
AC^2=4a^2-a^2
AC=√3a^2
Calculons GA
GG1^2+G1A^2=GA^2
(√3a^2/2)+a^2=GA^2
GA^2=3a^2/4 + a^2
GA=√7a^2/2
Calculons GB
GG1^2+G1B^2=GB^2
3a^2/4 + 4a^2=GB^2
GB^2=19a^2/4
GB=√19a^2/2
Calculons GC
GG2^2+G2C=GC^2
a^2+3a^2/4=GC^2
GC^2=7a^2/4
GC=√7a^2/2
Question 2a
f(M)=3(MG+GA^2)-2(MG+GB^2)+MG+GC^2
f(M)=3MG-2MG+MG+3GA^2-2GB^2+GC^2
f(M)=2MG+3*7a^2/4-2*19a^2/4+7a^2/4
f(M)=2MG+21a^2/4-19a^2/2+7a^2/4
f(M)=2MG-6a^2
Question
2a déterminer et construire l ensemble (T) des points M du plan tels que
f(M)=2a^2
Je ne comprends pas
Bonjour moussolony.
Dans ta formule de f(M), MA et MC, ils ne seraient pas au carré par hasard ?
J'ai trouvé comme toi pour GA, GB et GC.
En France, je crois que les barycentres ne sont plus au programme de terminale (et je trouve cela dommage car j'aimais beaucoup les barycentres). Tu es d'où ?
Sachant que, pour tout M du plan, ,




.
Du coup, quel est l'ensemble (T) des points M du plan tels que ?
Elles sont correctes à condition que , avec toutes les longueurs au carré, et pas seulement MB comme tu l'as marqué.
Pour h(M) aussi ? Du coup on essaie la suite ? Je ne te promets rien, ça fait super-longtemps que je n'ai pas fait un tel exercice 
Avec un compas que tu ouvres de la longueur 2a et que tu piques en G, bien sûr.
Par contre, je suis très ennuyée pour la question d'après, je crois que tu trouveras mieux que moi !
Est-ce que tu peux bien revérifier l'énoncé ?
Pour , je crois que c'est bon.
Mais pour , c'est bête car moi je trouve un vecteur
tel que
, pas
.
Mais vu la suite de l'énoncé, ça doit bien être
Pardon, j'ai fait des fautes de frappe :
Trouver un vecteur tel que
Mon idée, c'était de décomposer et
dans l'expression de h(M) à l'aide de la relation de Chasles, mais je ne trouve pas les
, seulement
!
Je crois qu il doit avoir une erreur de frappe. Mais c est un exercice de maison.
Mais comment vous trouvez -a^2
J'écris :
Ce qui me donne :
Mais pour les , je sèche. As-tu une idée, toi ? Ou des gens qui passeraient par là ?
Ça ne va pas du tout, car GEC et GFC sont loin d'être équilatéraux, même si  était la médiatrice de [GC].
était la médiatrice de [GC].
Je vais essayer de voir si on peut trouver cet énoncé sur internet, ou peut-être dans un de mes vieux livres avec les barycentres ? Mais ça m'étonnerait car je les ai presque tous donnés.
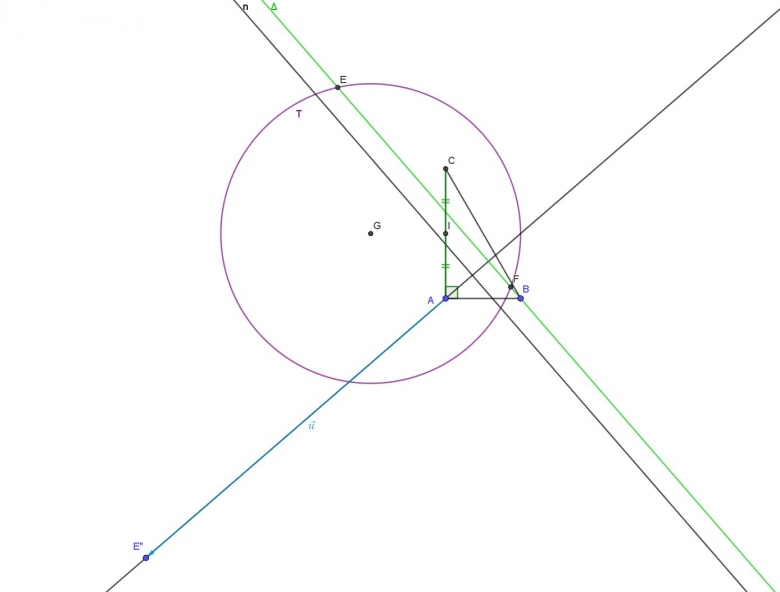
Ça y est, j'ai trouvé quelle erreur s'est glissée dans l'énoncé !
L'exercice semble fonctionner si c'est AC et non BC qui vaut 2a !