Le fichier est accessible ici : ***

édit Océane : si tu veux de l'aide, mercide faire l'effort de recopier ton énoncé sur le forum

tu dois donc obtenir quelque chose du genre :

x = g(t)
y = h(t)

et vouloir démontrer que y = f(x) ?

...

Et bien, j'ai pensé à calculer les coordonnées de Gt.
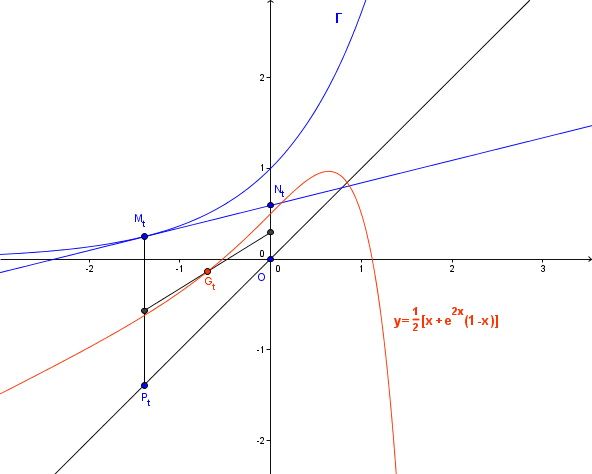
J'ai donc trouvé les coordonnées de Mt (t,e^t) Pt (t,t) et Nt (0,te^t) mais je ne suis pas sûre pour Nt. Puisque par hypothèse, Nt coupe l'axe des ordonnées, son abscisse est forcément nulle. De plus, comme Nt appartient à la tangente de la courbe de exp(t), je dirais que son ordonnée est égale à l'équation de la tangente au point d'abscisse t.

Ensuite, il faudrait que je trouve les coordonnées de Gt, barycentre de ces trois points. Sauf que là encore je bloque.

Bonsoir,

Tu devrais poster ton énoncé ...

Dans le plan muni d'un repère orthonormal (O, i, j), on considère la courbe T d'équation y = exp(x) et la droite D d'équation y = x.

1) Soit t un réel ; on désigne par Mt le point de T d'abscisse t.
La tangente à T au point Mt coupe l'axe des ordonnées au point Nt.

2) On désigne par Pt le point de D d'abscisse t et par Gt l'isobarycentre des points O, Mt, Pt et Nt. Le point Gt est donc le barycentre des points pondérés (O,1), (Mt, 1), (Pt,1) et (Nt,1)
a) A l'aide d'un logiciel de géométrie plane, placer les points M-2 ; P-2 et N-2 puis construire le point G-2.
b) Idempour G1.
c) Tracer l'ensemble des points GT quand t décrit R.

Ne dois-je pas utiliser les formules :
xG = (axA + bxB + cxC + dxD) / a + b + c +d
pour trouver les coordonées de G ?

Bonjour,

L' équation de la tangente en d' abscisse à :



Coordonnées de ; dans l' équation précedente:



et

D' où les coordonnées de :





Donc que l' on remplace dans l' expression de pour obtenir:



qui est l' équation de la courbe décrite par quand décrit

Merci infiniment cailloux !

De rien Marion93