- Un Cours sur les ensembles mathématiques - seconde
- Cours sur les nombres, les ensembles et les nombres premiers - seconde
- Rappel sur les nombres premiers suivi de neuf Exercices d'application - seconde
- Cours sur les valeurs absolues, les encadrements, les distances - seconde
- Petit Exercice d'initiation aux valeurs absolues - seconde
Inscription / Connexion Nouveau Sujet
calcul
bonsoir j'ai exercice qui me fatigue
soit N le nombre qui s'ecrit en juxtaposant, dans l'ordre, les 2017 premiers entiers naturels non nuls:
N=12345678910111213......2014201520162017.
1- calculer le nombre de chiffre de N
2- quel est le chiffre qui occupe la2017eme place en partant de la gauche?
bon j'ai essaye de traiter le 1 et j'ai trouve 6961chiffres mais je ne sais pas si c'est ca ou pas
Bonjour
Sujet intéressant. Je n'ai pas de solution miracle à t'apporter, juste une piste à peut-être étudier : j'ai fait un tableau avec les places des différents chiffres qui apparaissent dans le nombre N
Je ne sais pas si cela peut mener ou pas vers une solution
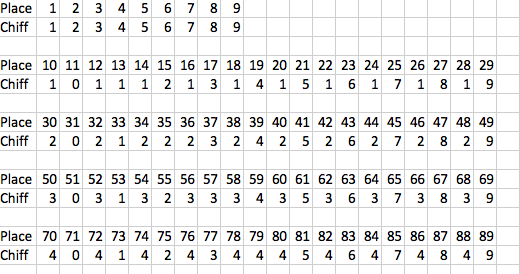
Bonjour, j'ai une idée :
de 1 à 9 on a : 1×10-1 chiffres ;
de 10 à 99 ona : 2×10^2 chiffres;
de 100 à 999 on a: 3×10^3 chiffres :
de 1000 à 2000 ona : (4×10^4)/10=4×10^3 chiffres ;
de 2001 à 2017 on a: 17×4 chiffres.
Bonsoir,
J'ai trouvé un nombre N légèrement différent du tien, peux-tu nous dire comment tu as fait?
Voici ce que j'ai fait pour la question 1):
D'abord tu as les 9 premiers chiffres (de 1 à 9), puis tu as les nombres allant de 10 à 99 (il y en a 90) avec 2 chiffres, ce qui fait 90x2 nouveaux chiffres. Tu as encore les nombres allant de 100 à 999 (900 exactement) avec 3 chiffres, soit 3x 900 et enfin tu as 1016 nombres entre 1000 et 2017 avec 4 chiffres, soit 4x1016 nouveaux chiffres.
J'ai donc:
9 + 90x2 + 3x900 + 4x1016
soit N=6953
Pour la 2) je ferais comme ceci:
Tu pars de la droite, tu sais que tes 4064 derniers chiffres sont ceux des nombres allant de 1000 à 2017, tu les enlèves, et il ne te reste plus que 2889 chiffres.
Ensuite, tu dois enlever 2889- 2017= 872 nombres qui sont des nombres de 3 chiffres.
or 872=290 (avec un reste de 2), ce qui signifie que tu enlève les 290 derniers nombres de 3 chiffres, et les deux derniers chiffres.
Si tu enlèves les 290 derniers nombres en partant de 999, tu t'arrêtes à 709, et comme tu enlèves encore 2 chiffres, tu vois que le dernier chiffre (ie la 2017e position) est 7
Donc je dirais que c'est 7, mais je me suis put-être trompé quelque part.
Bonsoir,
1000 et 2017 avec 4 chiffres, soit 4x1016
alberto13: de 1000 à 2017 il y a 1018 nombres, soit 6961 au total
Bonsoir,
1000 et 2017 avec 4 chiffres, soit 4x1016
alberto13: de 1000 à 2017 il y a 1018 nombres, soit 6961 au total
Au temps pour moi




