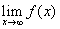Inscription / Connexion Nouveau Sujet
calcul d'aire (comprise entre 2 fonctions)
voila, on me demande de calculer l'aire comprise entre y=x+sinx, x=0, y=0 et x=
comme réponse, j'obtiens (²/2)+2 = 6,934...
est-ce juste? 
merci de me répondre et bonne journée!
merci
j'ai d'autres questions dans ce genre:
alors,
1) aire délimitée par la rosace d'équation polaire p=2sin
pour allant de 0 à (/2)
j'obtiens: 0 mais la il y a un problème.
0/2 2sin2 d ? on commence comme cela?
alors ensuite en utilisant l'intégraiton par substitution j'obtiens t=2 et dt=2d
ce qui me fait au final [-cos2]0/2
je calcule, j'obtiens 0... je trouve pas mon erreur...
Bonjour,
Je suppose que ton calcul d'intégrale est juste (je n'ai pas vérifié).
Dans ce cas, [-cos2]0 /2 = 1 - (-1) = 2
euh oui vous avez raison, je sais pas pourquoi je trouvais 0... erreur de calcul
merci ! si vous voulez j'en ai encore 
je ss entrain de les faire :p
l'aire comprise entre le cercle x²+y²=4 et la parabole y²=3x 
je mets les réponses après!
enfait non mais je ne sais pas dans quelle forum le mettre. Je suis de belgique en première architecture. J'ai certains exercices à faire qui sont du nvx terminale et d'autre pas..
qq'un a fait le calcul pour le cercle et la parabole? j'obtiens 64,6494 mais ca parrait bcp trop... :p
alors voila mon raisonnement:
pour trouver les points d'intersections:
y=
(4-x²)
y²=3x
donc 4-x²=3x
donc x²+3x-4=0
on cherche les racines... j'obtiens x=1 et X=-4
je remplace dans une équation pour trouver les y.
finalement j'ai (1,+-3) et l'autre n'existe pas car en remplacant x par -4 j'ai -12. donc pas possible...
je commence à intégrer...
S/2=043x-(4-x²)
S=042(3x-(4-x²))
=042.(3x1/2 - (4-x²)1/2
=[2.((6x3/2)/3)-2.((8-2x²)3/2/3)]04
etc... mais a mon avis j'ai déja bcp de fautes dans ce que je viens d'écrire... :p
désolé, petit problème, comment supprimer un message ? :-s
les bornes, je les trouve en faisant un graphique du cercle et de la parabole...
mais ca semblai assez bizarre.. les vrais bornes seraient 1 et -4?
Pour moi, les bornes sont 0 et 2 (le cercle est de rayon 2).
Ensuite, on découpe l'intégrale en 2 parties : de 0 à 1 avec la fonction y2 = 3x puis de 1 à 2 avec l'équation du cercle.
oui ca parrait bcp plus logique comme cela! qq'un saurai me donner les calculs par hasard? ca m'aiderai bcp pour comprendre le reste de la matière que je dois encore voir autrement, je m'arrangerai
Je n'avais rien calculé mais il me semblait que (question du 10-08-09 à 15:41) l'aire délimitée par la rosace d'équation polaire p=2sin(theta) pour theta allant de 0 à (Pi/2) était un demi disque de centre (0 ; 1) et de rayon 1.
Son aire serait alors = Pi/2 unité d'aire
rapide calcul a posteriori :
Aire = 1/2 * S(de 0 à Pi/2) Rho².d(theta)
Aire = 1/2 * S(de 0 à Pi/2) 4.sin²(theta) d theta
= S(de 0 à Pi/2) (1 - cos(2theta)) d theta
= [theta - (1/2).sin(2theta))](de 0 à Pi/2)
= Pi/2 unité d'aire.
-----
Me trompe-je ?
Pour la première intégrale, pas de difficulté (primitive en x3/2)
Pour l'autre, on fait un changement de variable x = 2sin avec 
[/6 ; /2]
Finalement, je trouve S = 2/3 - 1/3
Désolé mais je ne maitrise pas assez Latex pour développer mes calculs 
Alors:
@ J-P Pourquoi intègre-t-on Rho²?
@ godefroy_lehardi Je n'ai pas fait les calculs, mais je te fais confiance et je suis d'accord sur le changement de variable et tout. On pouvait cependant peut-être faire plus simple par des considérations géométriques...
Pourquoi intègre t-on Rho² ?
D'abord un raisonnement physique simple que tous devraient avoir comme réflexe.
Une aire à les dimensions de L² (longueur au carré)
Comme un angle (theta) n'a pas de dimension (il a une unité mais pas de dimension), une intégrale de Rho * d(theta) n'a pas la dimension L² et ne peut donc pas être une aire.
Par contre, une intégrale de Rho² * d(theta) a bien la dimension L² d'une aire.
Donc le calcul initial est forcément faux.
-----
Voir sur ce lien : 
qui rappelle la formule :
Annuler
connectez vous