Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale Limites de fonctionsTopics traitant de Limites de fonctions [tout]Lister tous les topics de mathématiques
Niveau terminale
Partager :

Calcul d'une limite trigonometrique

Posté par
Dududuu13 03-10-20 à 18:02

Bonjouur!!
Du coup ça fait 1h que je coince en une limite. J'ai le corrigé mais la correction ne montre pas les démarches qu'il faut suivre. Voici l'equation attachée.
Je sais qu'il existe unecertaine l'hôpital's rule mais on a pas vu ça. Je dois montrer une des limites bien connues (comme sin(x)/x) ) mais j'ai binen a essaier je ne sais pas comment retrouver mon chemin.

Merci beaucoup!

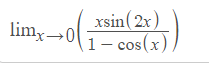
Calcul d\'une limite trigonometrique

Posté par
malou Webmasterre : Calcul d'une limite trigonometrique 03-10-20 à 18:10

Bonjour
tu as tout ce qu'il faut pour écrire des maths sur notre site
je te conseille l'éditeur Ltx
Calcul d\'une limite trigonometrique


c'est assez intuitif
des premières explications ici : [lien]

Posté par
Dududuu13re : Calcul d'une limite trigonometrique 03-10-20 à 18:13

*malou>citation inutile supprimée*
Ah merci beaucoup! je n'étais pas au courant de ça, dsl!!

Posté par
Pirhore : Calcul d'une limite trigonometrique 03-10-20 à 18:43

Bonjour,

remplace sin(2x) par une formule en fonction de x

1-cos(x) =? en fonction de \dfrac{x}{2}

Posté par
Dududuu13re : Calcul d'une limite trigonometrique 03-10-20 à 19:31

Pirho @ 03-10-2020 à 18:43

Bonjour,

remplace sin(2x) par une formule en fonction de x

1-cos(x) =? en fonction de \dfrac{x}{2}

Bonjour,
j'ai essayé mais ça me remets toujours a la forme indéterminée

Posté par
Priamre : Calcul d'une limite trigonometrique 03-10-20 à 20:40

Bonsoir,
Qu'as-tu écrit, plus précisément ?

Posté par
Pirhore : Calcul d'une limite trigonometrique 03-10-20 à 20:41

non mais montre un peu

Posté par
Dududuu13re : Calcul d'une limite trigonometrique 04-10-20 à 11:56

Bonjour, dsl pour le retard!

Je pense avoir trouvé la solution.
On a xsin(2x) = x^2*\frac{sin(2x)}{x}
Ceci va montrer la limite usuelle qui est \lim x\rightarrow 0 \frac{sin(2x)}{x}=a
Du coup si on divise toute l'équation par x^2 on va aussi avoir la relation \lim x\rightarrow 0 \frac{1-cos(x)}{x^2}=\frac{1}{2}
du coup on va avoir \lim x\rightarrow 0 \frac{\frac{sin(2x)}{x}}{\frac{1-cos(x)}{x^2}} = \frac{\frac{2}{1}}{2} = 4

Est-ce que cette démarche est correcte? Merci, et encore DSl pour le retard!

Posté par
alb12re : Calcul d'une limite trigonometrique 04-10-20 à 12:01

salut,
redaction approximative mais ton raisonnement est correct

Posté par
Dududuu13re : Calcul d'une limite trigonometrique 04-10-20 à 12:04

j'ai eu un peu de mal avec l'assistant latex, mais j'expliquerai mieux la démarche sur mon  cahier x)
merci beaucoup pour l'aide!


Rechercher
Menu
Espace membre
21 visiteurs
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1736 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !