Inscription / Connexion Nouveau Sujet
Calcul dans l'espace avec un tetraèdre trirectangle
Bonjour, oui c'est encore moi ; notre prof de maths n'a pas chômer avec les devoirs maisons ces derniers temps.. J'en profite donc pour vous exposez le dernier en date, presque identique au précédent.
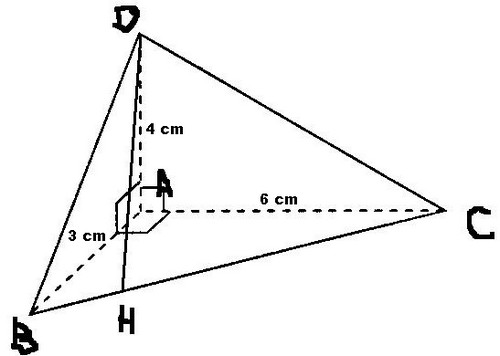
Voici ci-dessous le tetraèdre trirectangle à étudier :
1. Quel est le volume de ce tetraèdre ?
2. a. Calculer BC et en déduire sin A^BC.
b. H étant la hauteur issue de A dans ACB, déduire de la question 2a.la distance AH puis calculer CH.
c. On admet que DAH est rectangle en A calculer DH.
d. Montrer que HDC est rectangle en H.
e. Calculer l'aire du triangle BDC.
3. Déduire de 1 et 2e. la longueur de la hauteur issue de A du tetraèdre.
Pas de soucis majeur, mais des valeurs exactes sont éxigées.. Alors déja, pour AH je trouve 3sin(2V5/5). Le truc c'est que après, avec des valeurs comme ca je comprends plus rien.
Par exemple pour calculer CH on peut utiliser Pythagore dans AHB rectangle en H, mais il faut donc utiliser cette fameuse distance AH.. Quelqu'un pourrait-il m'aider à résoudre ce problème ? 
Bonjour,
les valeurs exactes sont justement celle où tu laisse une racine carrée sous sa forme initiale sans chercher à en calculer une valeur qui sera forcément approximative si la valeur qui est sous le radical n'est pas un carré
Par contre, je ne coprends pas très bien pourquoi tu t'encombres d'un sinus pour la longueur de AH
AH est forcément la hauteur dans le triangle ABC rectangle donc
AH*BC=AB*AC=18 (les deux manières de calculer le double de l'aire du triangle)
BC=3 5
5
donc AH=6 5/5
5/5
Oh super, merci Gaa! c'est vrai que ce sinus m'encombrait -.-
Par contre, pour la question 2e et 3 je vois pas comment on peut faire étant donné que je vois pas la hauteur dans le triangle BDC.
Mais DH est la hauteur du triangle BDC
en effet DA est perpendiculaire au plan ABC donc orthogonal à (BC)
(AH) est perpendiculaire à (BC)
donc le plan DAH est perpendiculaire à (BC) et donc (DH) est perpendiculaire à (BC)
On a calculé AH et on connait DA
tu peux donc par Pythagore calculé DH et aire DBC=DH*BC/2
pour la dernière question, tu exprimes le volume du tétraèdre de deux manières différentes
V=DA*aire ABC/3=(hauteurissue de A)*(aireDAB°/3


