Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques SupérieurOn parle exclusivement de maths, pour le supérieur principalement, les BTS, IUT, prépas... Licence Maths 1e ann StatistiquesTopics traitant de statistiques [tout]Lister tous les topics de mathématiques
Niveau Licence Maths 1e ann
Partager :

Calcul de covariance dans une distribution à deux dimensions

Posté par
alpharomeo 13-06-14 à 21:53

Bonsoir !

Je rencontre un sérieux problème avec un cours de statistiques que je dois réviser, je comprends absolument tout sauf une formule, celle de la covariance !

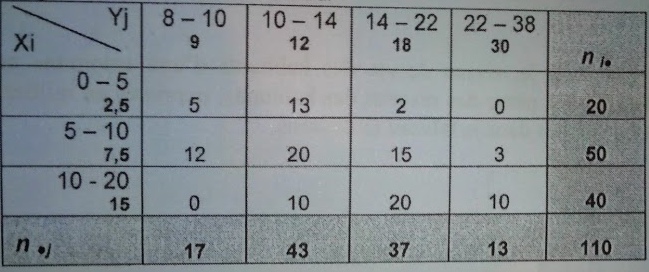
J'ai attaché la distribution à mon message, je sais tout calculer mais j'ignore comment calculer à la fois plusieurs sommes cela me rend fou.

Merci pour votre aide

Calcul de covariance dans une distribution à deux dimensions

Posté par
alpharomeoFormule covariance 13-06-14 à 21:55

J'ai attaché une image de la formule donnée, je rencontre là un problème de logique puisque je sais obtenir les différentes valeurs nécessaires au calcul mais ne sais pas comment m'y prendre pour calculer cette covariance ! Merci

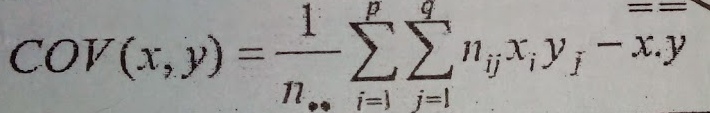
Formule covariance

Posté par
lafol Moderateurre : Calcul de covariance dans une distribution à deux dimension 14-06-14 à 00:41

Bonjour

la double somme, c'est juste qu'il faut calculer pour chaque case du tableau le produit du nombre qui est dans la case par celui en en-tête de la ligne contenant la case et par celui en en-tête de la colonne contenant la case, puis additionner tous ces produits.

Posté par
veledare : Calcul de covariance dans une distribution à deux dimension 14-06-14 à 01:09

bonsoir,
*le calcul de \bar X ,\bar Yles moyennes de X et Y est simple

pour la moyenne de X tu utilises la première et la dernière colonne de ton tableau elles représentent la distribution marginale de X
X_i   n_{i,.} \\ 2,5   20 \\ 7,5   50 \\ 15    40

\bar X=\frac{2,5*20+7,5*50+15*40}{110}=..

pour la moyenne de Y tu utilises la première ligne et la dernière ligne du tableau elles représentent la distribution marginale de Y

**pour calculer la somme double
tu peux calculer les produits correspondant à chaque ligne i et en faire la somme

pour X_i=2,5 cela donne
\frac{1}{110}(2,5)(9*5+12*13+18*2+30*0)=..

pourX_i=7,5
\frac{1}{110}(7,5)(9*12+12*20+18*15+30*3)=..

pourX_i=15
\frac{1}{110}(15)(9*0+12*20+18*15+30*10)=..

et tu ajoutes les trois sommes précédentes
tu peux aussi faire le calcul en utilisant les colonnes

Posté par
veledare : Calcul de covariance dans une distribution à deux dimension 14-06-14 à 01:10

bonsoir lafol,je n'avais pas vu que tu étais là

Posté par
alpharomeoMerci mais résultat 14-06-14 à 12:51

Merci beaucoup veleda pour ces explications.

Néanmoins après avoir réalisé les divers calculs (j'obtiens pour la moyenne de Xi 9,32 et Yi 15,68) j'obtiens cela :
(5,36 + 48,27 + 110,45) - 9,32*15,68 = 17,9424

Or il est dit dans l'énoncé que le résultat de cov(x,y) est 13,88

Ai-je fait une erreur de calcul quelque part ? Merci

Posté par
alpharomeore : Calcul de covariance dans une distribution à deux dimension 14-06-14 à 12:56

Je m'étais trompé ! Je trouve bien Cov(x,y) = 13,88 !

Merci encore pour votre aide !

Posté par
veledare : Calcul de covariance dans une distribution à deux dimension 14-06-14 à 14:01

je t'en prie,
bon courage pour les examens

Posté par
chabsnrdre : Calcul de covariance dans une distribution à deux dimension 18-04-18 à 20:34

bonjour, je suis navrée de remonter ce post mais j'ai exactement le même problème seulement moi je reste bloquée sur 17,9424 où est mon erreur ?

Posté par
lafol Moderateurre : Calcul de covariance dans une distribution à deux dimension 18-04-18 à 22:25

veleda @ 14-06-2014 à 01:09

bonsoir,
*le calcul de \bar X ,\bar Yles moyennes de X et Y est simple

pour la moyenne de X tu utilises la première et la dernière colonne de ton tableau elles représentent la distribution marginale de X
X_i n_{i,.} \\ 2,5 20 \\ 7,5 50 \\ 15 40

\bar X=\frac{2,5*20+7,5*50+15*40}{110}=..

pour la moyenne de Y tu utilises la première ligne et la dernière ligne du tableau elles représentent la distribution marginale de Y

**pour calculer la somme double
tu peux calculer les produits correspondant à chaque ligne i et en faire la somme

pour X_i=2,5 cela donne
\frac{1}{110}(2,5)(9*5+12*13+18*2+30*0)=..

pourX_i=7,5
\frac{1}{110}(7,5)(9*12+12*20+18*15+30*3)=..

pourX_i=15
\frac{1}{110}(15)(9*0+12*20+18*15+30*10)=..

et tu ajoutes les trois sommes précédentes
tu peux aussi faire le calcul en utilisant les colonnes


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1768 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !