Inscription / Connexion Nouveau Sujet
Calcul de volume
Bonjour,
Pourriez vous m'aider à résoudre cet exercice svp ?
Voici l'énoncé :
Déterminer le volume du solide obtenu par révolution autour de l'axe [Oy) du domaine limité sur l'intervalle [-1 ; 0] par l'arc de cercle de centre O et de rayon 1, sur l'intervalle [0 ; π/2] par la courbe d'équation y = cos(x).
Donner une valeur approchée à 10^-2 près de ce volume en cm^3 si l'unité graphique est de 2 cm.
Je ne suis pas sûr d'avoir compris l'énoncé, donc méfiance sur ce qui suit.
a) En se limitant dans les y >= 0
Le volume engendré par la rotation autour de [oy) de la courbe du demi cercle est entièrement englobé dans le volume engendré par la rotation autour de [oy) de la courbe du cos(x).
Il faut pour le montrer (je ne l'ai pas fait) démontrer que sur [-1 ; 0] (ou bien sur [0 ; 1]).
Donc on aurait
Si 1 unité de longueur = 2cm
On aurait alors
On aurait alors
b) si on doit aussi prendre en considération les y < 0.
Pour y < 0: Le volume engendré l'est uniquement par le demi cercle sous l'axe des abscisses.
Le volume est une demi sphère de rayon = 1
V' = (2/3).Pi.1³ = (2/3).Pi
Si 1 unité de longueur = 2cm
On aurait alors
c)
Le volume total serait donc = V + V'
-----
Comme je ne suis pas sûr que c'est ce qui était attendu, je ne vais pas plus loin.

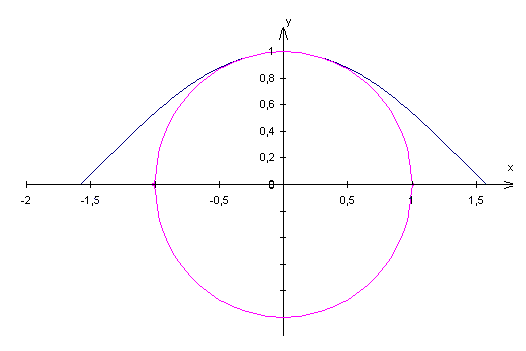
La courbe qui est avec l'exercice est composée du quart de cercle pour y positif et x négatif et de la courbe cosinus de x = 0 à x = 1.5.
Merci pour votre aide mais comment l'utilisé avec la courbe précédente?
Si j'ai bien compris, il n'y a rien du coté des y négatifs.
On ne regarde alors que la moitié supérieure de mon dessin ou si tu veux, le dessin joint à ce message.
Si on fait tourner la courbe représentant le cos(x) sur [0 ; Pi/2] autour de l'axe des y, on voit bien comme je l'ai dit avant que le volume que cela engendre englobe entièrement le volume engendré par la rotation du 1/4 de cercle autour de l'axe des y.
Donc le volume total est celui engendré par la courbe de cos(x) sur [0;Pi/2] qui tourne autour de l'axe des y. On peut "oublier" le quart de cercle.
On a alors y = cos(x) (x = 0 -> y = 1 et x = Pi/2 -> y = 0)
avec x = arccos(y)
Ma calculette donne V = 3,5864... unité de volume.
Si 1 unité de longueur = 2 cm, on a alors:
V = 2³*3,5864... = 28,69... cm³
----
Il reste à retrouver ce résultat en résolvant l'intégrale.
Je reste un peu sceptique sur cet exercice.
Es-tu bien sûr que ce n'est pas plutôt autour de l'axe des x qu'il faut faire tourner ?
Ce serait alors sans problème.

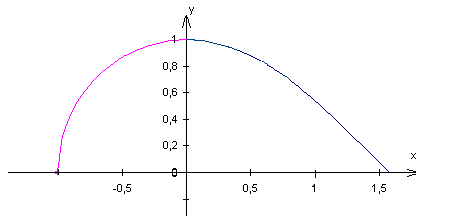
oui c autour de l'axe Ox c'est vrai que sa change tout!désolé


