Salut

Pour calculer l'aire sous une courbe, on découpe le domaine en une infinité de rectangle dont la somme tend vers l'aire. La somme des aires de ces rectangles définie l'intégrale de la courbe.

Pour une boule on fait la même chose, sauf qu'au lieu de découper la boule en rectangle, on la découpe en une infinité de disque. La somme des surfaces de ces disques correspond à l'aire de la boule.

Ainsi où A(z) est l'aire du disque inscrit dans la boule et de centre (0,0,z).
il faut juste trouver le rayon de ces disques.
Or si le disque est centré en (0,0,z) et est inscrit dans la boule, par Pythagore on trouve que son rayon vaut sqrt(R²-z²)

D'où

On calcule ça et on trouve . Magique.

bonjour

prends un disque infinitésimal d'épaisseur dz et de rayon Rcos(p) qui se trouve à la hauteur z=Rsin(p) p étant un angle élément de ]-Pi/2,Pi/2[:

l'élément de volume dV=dSdz
où dS est le surface du disque dS=(Rcos(p))²Pi et dz=Rcos(p)dp
donc
dV=PiR^3(cos(p))^3dp
cos((p))^3= cos(p)cos²(p)=cos(p)(1-sin²(p))=cos(p)-cos(p)sin²(p)
donc
V=Int(-Pi/2àPi/2)(dV=
=Int(-Pi/2àPi/2)[PiR^3cos^3(p)]dp
=PiR^3Int(-Pi/2àPi/2)(cos(p)-cos(p)sin²(p))dp
=PiR^3(2-(2/3))
=PiR^3(4/3)
=(4/3)(PiR^3)
------
voila

pourquoi le rayon est de R cos(p) et à quoi correspond cet angle p ???

Rebonjour
p est l'angle (OP,Ou);P est un point du cercle frontière du disque et ou le plan méridien qui passe par P.
la projection de P sur Oz et Ou donne (Rcos(p),Rsin(p)) donc le rayon du disque est Rcos(p) et la côte de P est z=Rsin(p)

essaies de faire un schéma stp

Bonjour  Nightmare
quel(le) étourdi(e)!!!
le plus magique c'est d'exprimer une aire en m!!!!
bravo pour utilisation du Latex

Je n'ai pas compris ta remarque Labo

Oups oui maintenant j'ai compris, je corrige cela !

Merci beaucoup.
Comment calculer le volume d'une pyramide régulière à base carrée de coté a et de hauteur h ?

Merci beaucoup de votre aide.

C'est la même idée, sauf qu'au lieu de la découper en disque tu vas la découper en... ?

je n'y arrive pas pour la boule. Je n'arrive pas  à trouver la primitive de  R²-z²

pour la pyramide à base carrée:

tu la tournes à l'horizontale, couchée sur le sol en quelque sorte:
Considère maintenant ta base (fais une figure dans le plan c'est plus simple), dont les sommets sont à (0;a/2) et (0;-a/2)

tu vas intégrer les aires de tes carrés, dont la longueur du côté évolue suivant deux droites d1 et d2 (comprises entre 0 et h), dont chacune s'annule en h

L'équation de d1 est y = -1/2 a/h * x + a/2   et d2: 1/2.a/h + a/2
essaye de finir maintenant, c'est le même principe que pour la sphère.

yoyodada > Pourquoi faire si compliquer ?

On garde la pyramide droite, on la découpe infiniment par des plans horizontaux d'hauteur z < h On obtient des carrés d'aire
On en déduit le volume de la pyramide en sommant continument :

erreur:

d2: 1/2. a/h - a/2

Nightmare:

tu as raison, mais le principe est exactement le même sinon, à savoir intégrer des segments de droites!

c'est vrai c'est un peu complexe mais ca marche bien !

Oui c'est vrai qu'au final cela revient au même

Pour répondre à Estelle : R² est une constante, donc je ne vois pas pourquoi l'intégration de R²-z² te bloque!

pour la boule:

l'équation d'un cercle dans le plan est x²+y² = R², donc y = racine(R² - x²).

pour le volume de la boule de rayon R entre x=-R et x = R:

Comme tu intégres l'aire formée par les disques de rayon évoluant suivant r(x) = racine (R² - x²), et comme la valeur de l'aire vaut A = pi.r(x)² = pi.(R²-x²)

donc tu intégres entre -R et R la fonction pi.(R²-x²)
en sortant la constante pi, ca te donne
V = pi.int(-R ; R) de R² - x² .dx = [R²x - x^3/3 ] entre -R et R.
soit V = pi. (R^3 - R^3 /3 + R^3 -  R^3/3)
V = pi. (4/3 R^3): inutile d'utiliser le cos.

j'avais oublié que R²est une constante.
La primitive est donc R²z-(z³)/3

C'est bien ça (Une primitive, cela dit)

Merci, j'ai réussi pour la boule.

Nightmare: A quoi correspond le b dans ton intégration pour le volume de la pyramide, tu a ab*z²/h²

Oui pardon, j'ai pris une pyramide à base rectangulaire.

ici b=a

ici a² et h², sont des constantes ? je dois donc trouver une primitive par rapport à z ?

Pour calculer int de 0 à h de a²* z²/h² dz,
est ce que je peux prendre comme primitive a²/3 * z³/h²


en derivant :
a²/3 * (3z²*h²)/h⁴
on simplifie par 3 et par h² et on retombe sur ce qu'on veut, à moins que j'ai fait une erreure ?

Déjà pour ne sors-tu pas a²/h² de l'intégrale? c'est une constante...

Ensuite il te reste à calculer l'intégrale de z² entre 0 et h, rien de difficile !

Merci beaucoup de m'avoir aidé.

je voulais savoir comment calculer le volume d'une pyramide a base triangulaire (ABC) de hauteur OH=h en considérant un plant de cote z qui coupe la pyramide et une homothétie de centre O et de rapport que l'on déterminera


  

Un dessin:



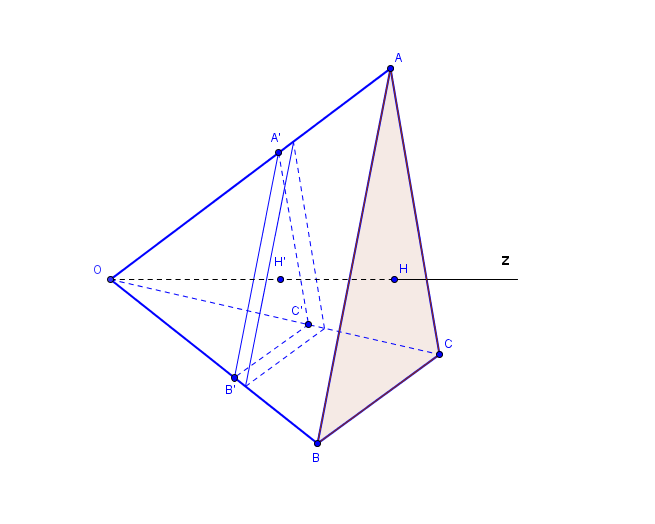
On découpe la pyramide en prismes élémentaires de hauteur et de base d' aire donc de volume

Soit l' aire de base de la pyramide.

Le rapport de l' homothétie qui transforme le triangle en le triangle vaut où est la hauteur de la pyramide.

Ainsi

et

Bonsoir Pierre

Je ne comprends pas :

Et dc z se détermine par rapport au plan passant par O et // au plan formé par la base de la pyramide, ie le trg ABC ; pas par rapport à cette base ABC ?

Merci de me dire

Salut Philippe !
Juste en passant :
Une homothétie de rapport k multiplie les logueurs par /k/ , les aires par k² et les volumes par k³
D'où ce z²/h².
Pour le reste, j'ai pas lu !!  

Bonsoir Géraud,

Eh bien ça me suffira pr avancer ce soir, merci

les volumes par |k³|, non ?

_{Tt va bien ; tu corriges des copies de bac cette année ?}

Exact pour la valeur absolue !!
_{Oui : Bac S ! ...Avec une merdouille dans l'exo 2, voir espace profs}

j'avais oublié la notion d'homothetie j'ai bien compris

merci cailloux

De rien boalexis.

Remarque qu' avec une pyramide de base quelconque (et pas seulement triangulaire), la méthode donne le même résultat: