Bonjour,
peux-tu joindre le dessin pour qu'on sache où sont situés les points I et V par rapport au carré ABCD

extrait de la FAQ du forum :

Q05 - Puis-je insérer une image dans mon message ? Comment faire ? Quelle image est autorisée ?

Vous souhaitez ajouter une image ou un pdf à votre message . Veuillez obligatoirement respecter ces règles :

Énoncé d'exercice ou de problème :

Pour les énoncés courts (moins de 5 lignes sur une feuille A4) :
La recopie est obligatoire.
L'option d'attachement d'image n'est donc à utiliser que pour représenter une figure, un tableau ou un graphique, pas du texte !

Pour les énoncés longs  :
Les 5 premières lignes sont à recopier pour aider l'archivage des sujets sur le site.
Cela fait, l'énoncé dans sa totalité, pourra alors être joint en image (choisir Img) ou en pdf (choisir Pdf ) mais dans le respect des droits d'auteurs en vigueur. Pour les pdf, merci d'en préciser la source.

Recherches (même non abouties) de l'exercice :
Elles doivent être obligatoirement recopiées, et ce, dès la demande d'aide.
l'option d'attachement d'image n'est donc à utiliser que pour représenter une figure, un tableau ou un graphique, pas du texte !
Les formats autorisés sont exclusivement les suivants : gif, jpg, jpeg, et png. La taille d'un fichier est limitée à 2 MO maximum pour une image et à 500 ko pour un pdf.

Le non respect de ces règles entraînera la suppression du contenu de votre sujet (même si des réponses ont été apportées) et éventuellement la suspension de votre compte !

Seule exception : Dans le forum détente, des réponses longues et élaborées , contenant plusieurs images explicatives, pourront être postées sous forme d'image ou de pdf. Les énoncés, quant à eux, devront toujours être rédigés sur le site (indispensable pour le référencement).

Il me dit que l'image est trop grosse, je n'arrive pas à la mettre 😭

Bonjour,

dans ce cas il faut la décrire entièrement et exactement

(= si tu ne sais pas qu'il y a des logiciels de traitement d'images, explorer les menus de Paint permet de s'en sortir et de savoir que ce logiciel ne sert pas que à faire des gribouillages sur un écran, et savoir qu'une photo est réellement un truc de taille monstrueuse donc normal que ce soit rejeté)

il y a deux positions possibles du triangle équilatéral ABI construit sur le côté d'un carré ABCD
tu dois préciser laquelle (à l'intérieur ou à l'extérieur du carré ??)
et pareil pour BCV

pour les coordonnées il faut être conscient de ce que veut dire réellement la définition de "coordonnées"
et les calculer dans ce cas c'est "visible" et calculer la hauteur d'un triangle équilatéral (Pythagore dans le demi-triangle)

ABI est construit à l'intérieur de ABCD et BCV est construit à l'extérieur de ABCD 😊

OK et donc qu'est ce qui te gène pour appliquer ce que j'ai dit (définition de "coordonnées dans un repère" et Pythagore)



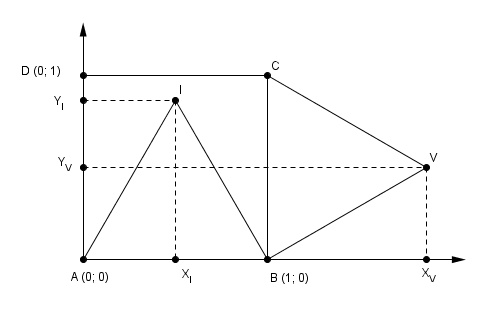
l'abscisse de I c'est la mesure de AX_I avec comme unité AB ("ATTENTION ON SE PLACE DANS LE RÉPÈRE (A;B,D)")
etc ...

Donc ça fait 0,5 en abscisse mais pour calculer l'ordonné?🤔