Inscription / Connexion Nouveau Sujet
Calcul vectoriel démonstration
Bonjour et merci de bien vouloir m'aider.
En fait,j'ai rencontré un problème sur cet exercice.
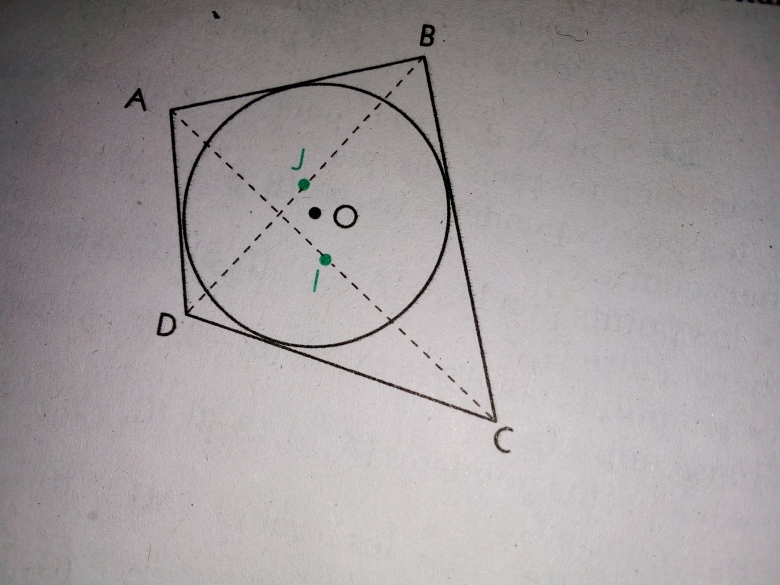
Soit ABCD un quadrilatère convexe admettant un cercle inscrit de centre O.
1.a) Démontrer que:
A(AOB)+A(COD)=A(BOC)+A(DOA)
b)En déduire que :vecteurOA^vecteurOB+vecteurOC^
vecteurOD=vecteurOB^vecteurOC+vecteurOD^vecteurOA
En fait ici je suis un peu bloquée parceque j'ai essayer de remplacer l'aire par son expression en fonction du produit vectoriel mais rien ça n'abouti pas j'arrive à
A(AOB)+A(COD)=(1/2)[vecteurOA^vecteurOB]+(1/2)[vecteurOC^
vecteurOD]
La deuxieme question est simple mais la première je n'arrive pas à démontrer.
Merci d'avance.
Remplace chaque Aire en fonction de leur hauteur h = R (rayon du cercle inscrit).
Et c'est quasiment terminé.
Remplace chaque Aire en fonction de leur hauteur h = R (rayon du cercle inscrit).
Et c'est quasiment terminé.
Comment pouvez vous savoir que le rayon est la hauteur des triangles?
Si je ne dis pas de bêtise, le cercle étant inscrit dans le quadrilatère, cela signifie que les côtés sont sécants en un unique point au cercle : les droites passant par les côtés du quadrilatère sont donc tangentes au cercle, donc par définition le rayon reliant le point sécant au centre est perpendiculaire au côté tangent.
Par définition : j'appelle le point d'intersection du côte
et du cercle, alors
.
Je me rappelle de ce genre d'exercice, lequel montre que les quadrilatères ayant cette particularité d'avoir un cercle inscrit se distinguent par deux égalités:
- les sommes des côtés opposés sont égales, donc ;
- les angles formés par les sommets et le centre du cercle sont 2 à 2 supplémentaires, soit
En revanche, je ne me souviens plus de la démonstration, si ce n'est l'utilisation d'un théorème... et ma mémoire flanche malheureusement car je ne me rappelle plus lequel ! Seul indice, c'est en relation étroite avec les surfaces.
Bonjour à tous,
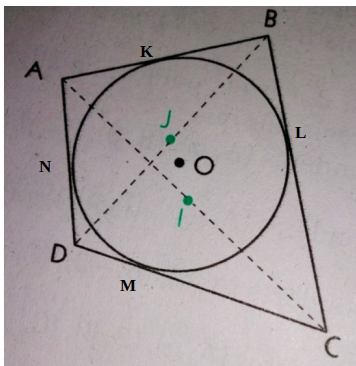
Je pense utile de donner des noms aux points de la figure.
Par exemple noter K, L, M, N les points de contact des côtés AB, BC, CD, DA avec le cercle.
Par propriété de la tangente à un cercle, on a les droites (OK) et (AB) perpendiculaires.
Ensuite, utiliser une autre propriété des tangentes :
Avec les 2 tangentes issues de A, on a AK = AN.
C'est ce qui permet de démontrer AB+CD = AD+BC 
malou edit > avec les points introduits par Sylvieg 
En fait ma question c'est plutot est ce ces triangles sont rectangles?pourquoi R est la hauteur?
Aucun triangle n'est rectangle.
Mais l'aire d'un triangle est donnée par : 1/2 * Base * Hauteur
Ici la hauteur de chacun des triangles est égale à R = Rayon du cercle inscrit.
Bonjour et merci Sylvieg !
Tout me revient d'un seul coup !
J'avais oublié cette important propriété de deux tangentes à un même cercle qui se coupent en un point : les distances entre le point d'intersection des tangentes et les points de contact au cercle sont égales, ce qui peut se démontrer par le théorème de Pythagore.
Les triangles et
sont rectangles en
et
, les côtés
et
sont rayons du même cercle donc de même longueur, et après tout s'éclaircit.
Maesen, je pense que tu as tout ce dont tu as besoin pour démontrer l'égalité de la première question.


 équivalences des systèmes de niveaux scolaires
équivalences des systèmes de niveaux scolaires
