bonsoir
ABCD est un rectangle de largeur 4 cm et de longueur 8 cm.
1)calculer la valeur exacte de l

la diagonale AC du rectangle?

2)ecrire sous la forme a racine carrée de 5 avec a entier.
svp aidez moi je ne connais rien svp faites quelque chose

d'après ce bon vieux pythagore...
diag=rac(8^2+4^2)=rac(80)=rac(5*16)=4*rac(5)

ouais ok... et est ce que c'est censé m'aider...

bonsoir yoshiman,

(Il y a des gens qui ne dorment jamais !)

L'équation d'une droite , c'est du cours.

Tu écris (en vecteur) AM=tAB    t

avec AM de coordonnées (x-x_A;y-y_A;z-z_A) et AB de coordonnées (x_B-x_A;y_B-y_A;z_B-z_A)
et en projetant sur les 3 axes de coordonnées tu obtiens une représentation paramétrique de cette droite sous la forme de 3 équations dont voici la première:

    x-x_A=t(x_B-x_A)     soit x=x_A+t(x_B-x_A)

On peut aussi définir une droite comme intersection  de 2 plans, mais généralement la méthode précédente est meilleure.

Merci de ta réponse. Je n'ai pas bien compris la partie sur les vecteurs mais les formules me suffisent tant que je réussis à les utiliser. (à suivre)

x-xA=t(xB-xA)     soit x=xA+t(xB-xA)
y-yA=t(yB-yA)     soit y=yA+t(yB-yA)
z-zA=t(zB-zA)     soit z=zA+t(zB-zA)

bonjour,
Connaître les formules, c'est bien, mais savoir les retrouver par une petite demonstration c'est mieux (la mémoire peut avoir des défaillances)

Deux vecteurs sont égaux s'ils ont les mêmes coordonnées dans un même repère.
Si tu as (en vecteur) U=V et si U (a,b,c) et V(a',b',c' ) alors a=a' b=b' et c=c'
Et si U=tV (t réel) alors les coordonnées de tV sont (ta', tb', tc') , on obtient a=ta' b=tb' et c=tc'.

Bonne rentrée

1) Besoin d'un éclairsissement pour le fun :

Quand tu dit U (a,b,c) est un vecteur ; il me semblait qu'un vecteur était défini par 2 points, donc dans le cas de U, le 2ème c'est l'origine du repère? Si c'est ça j'ai bien compris la suite. En tout cas comprendre cette partie n'est pas indispensable pour ce que je veux faire

2)Là une question pour laquelle j'ai un besoin vital de la réponse :

En fait je programme un jeu vidéo de combat spatial. Mon vaisseau tire des lasers (d'où mon besoin de connaitre l'équation d'une droite dans l'espace pour calculer la trajectoire des lasers).
Je connais le point de départ du laser (position du vaisseau) mais pas le point d'arrivée.
Or il me faut le point d'arrivée (ou au moins l'écart entre mon point de départ et un autre point de la droite) qui doit être multiplié à t dans les équations paramétriques.
J'arrive à le faire en 2D sans problème (sur un plan parallèle au plan Z avec des rotations autour de l'axe Y) mais dès qu'il s'agit de rotations 3D c'est la cata.
En 3D le vaisseau tourne à gauche ou à droite : rotation autour de l'axe Y (ce qui marche) ; mais il doit aussi pouvoir tourner ("plonger") vers le bas ou vers le haut : rotation autour de l'axe X.

Donc dans x=xA+t(xB-xA), y=yA+t(yB-yA), z=zA+t(zB-zA), mon problème c'est de pouvoir déterminer xB,yB,zB.

Sachant que les facteurs de t sont les écarts entre les point de départs et d'arrivée, j'avais fait ceci quand il s'agissait que de ne tourner qu'autour de l'axe Y : x=xA+t(sin(ANGY)), y=yA+t(0), z=zA+t(cos(ANGY)). J'ai essayé de modifier les facteurs en prenant compte de la deuxième rotation mais bon c'était pas ça (l'avantage en programmant des jeux vidéos c'est qu'on voit tout de suite quand ça va pas ).
Et donc la question : quelles sont les bonnes valeurs des facteurs quand on combine les 2 rotations?

ou s'il y a un autre moyen que trigo & co pour compléter les équations paramétriques, n'hésitez pas à me le faire savoir !

vous l'aurez certainement deviné mais bon pas le temps de jouer aux devinettes :

   -   ANGY est l'angle de la rotation autour de l'axe Y
   -   ANGX est l'angle de la rotation autour de l'axe X

Ce sont des précision que j'apporte à mes 2 précédents messages, donc veuillez bien lire ces 2 messages si vous arrivez ici directement.

bonjour,

Je vois qu'on est loin de l'équation d'une droite.

Pour la première question qui servira pour la seconde:

n'est pas un point de l'espace mais un vecteur . On peut l'étudier à travers l'un de ses représentants par exemple. C'est en quelque sorte le "générique". Il a une direction , un sens, une longueur, mais pas d'origine.C'est ,si tu veux une "flèche". Il est caractérisé par ses 3 coordonnées qui sont les projections de sur les 3 axes Ox, Oy, Oz.

Pour la question 2:

Si j'ai bien compris tu as besoin de l'equation de toutes les droites qui pivotent autour de A (ton vaisseau spatial).Cela te fera 4 paramètres.
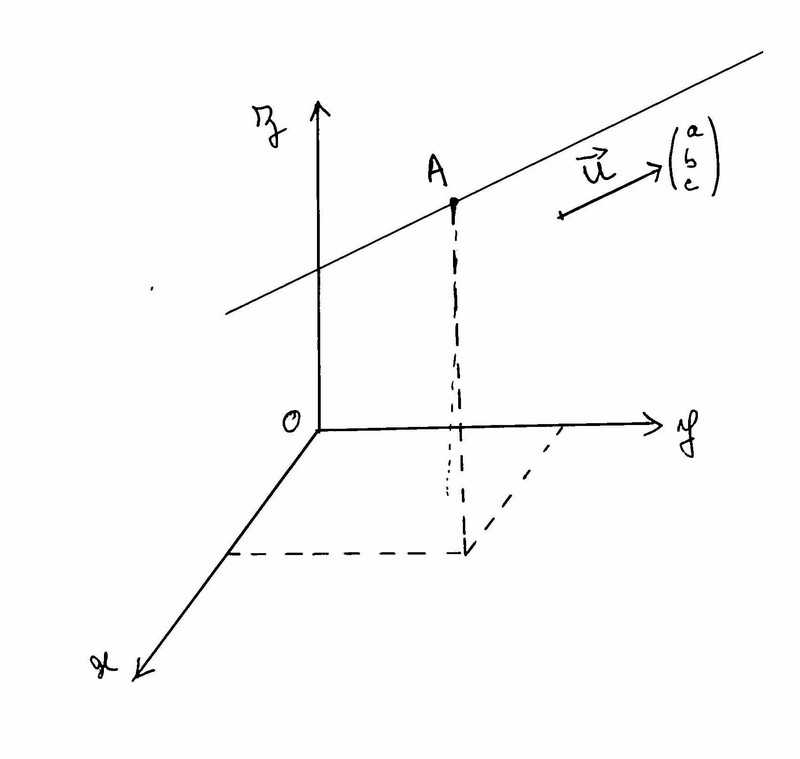
Soit un vecteur dont la direction et le sens sera celui de la droite passant par A (on parle alors de vecteur directeur), tu auras le système suivant:

avec (a,b,c) et t représentant la position d'un point sur cette droite

x=x_A+at
y=y_A+bt
z=z_A+ct

Si ton repère de référence est déterminé par (Ox,Oy,Oz), faire varier c fera pivoter ta droite au dessus ou au dessous du plan déterminé par (Ox,Oy) et la valeur de t donnera la position d'un point sur cette droite.
Si c=0 toutes tes droites passant par A seront dans un plan parallèle au plan (Ox,Oy).

Bon courage pour la suite

rebonjour,

Voici une figure élémentaire sur :repère, vecteur, droite ...

merci beaucoup de ton aide j'ai résolu mes problèmes depuis quelques heures. Je ne pense pas que les maths me poseront à nouveau problème dans mon jeu mais si ça arrive, je n'hésiterais pas à repasser^^