Annuler
connectez vous
- Bissectrice et cercle inscrit dans un triangle - Cours 4ème
- Exercice Bissectrices et cercles inscrits dans un triangle
- Cours sur les Figures planes, Distance d'un point à une droite et Tangente à un cercle
- QCM : Figures planes, distance et tangente - Exercice 4ème
- Six Exercices de géométrie pure - quatrième
Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques Collège cycles 3 /4On parle exclusivement de maths, niveau collège. QuatrièmeForum de quatrième GéométrieTopics traitant de géométrie [tout]Lister tous les topics de mathématiques
Niveau quatrième
cercle circonscrit exercice
Posté par mel02mel
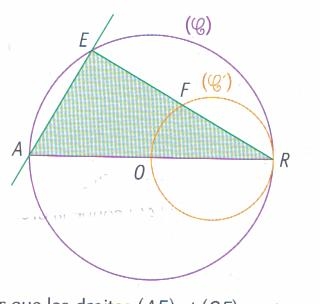
C est un cercle de centre O et de diamètre AR. C' est le cercle de diametre OR. Le point E appartient au cercle C. La droite ER coupe le cercle C' en F.
Démontrer que les droites AE et OF sont parallèles
Quelqu'un peut il m'aider ? Merci
Bonsoir ?
Si un triangle a un côté qui est le diamètre de son cercle circonscrit, alors ce triangle est...
Si tes triangles sont rectangles, tu dois avoir des angles droits, donc des droites perpendiculaires... Tu dois pouvoir te débrouiller avec la célèbre phrase que tu connais depuis la sixième "si deux droites sont perpendiculaires à une même troisième, alors elles sont ..."
Oui... Enfin, il faut quand même montrer que les deux droites sont perpendiculaires à une même troisième... 