Annuler
connectez vous
- Bissectrice et cercle inscrit dans un triangle - Cours 4ème
- Exercice Bissectrices et cercles inscrits dans un triangle
- Cours sur les Figures planes, Distance d'un point à une droite et Tangente à un cercle
- QCM : Figures planes, distance et tangente - Exercice 4ème
- Six Exercices de géométrie pure - quatrième
Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques Collège cycles 3 /4On parle exclusivement de maths, niveau collège. QuatrièmeForum de quatrième GéométrieTopics traitant de géométrie [tout]Lister tous les topics de mathématiques
Niveau quatrième
cercle et triangle rectangle
Posté par maximelillois
Bonjour à tous. Voilà j'ai un problème avec un de mes exercices de DM. Pouvez-vous m'aider ?
Voici l'énoncé :
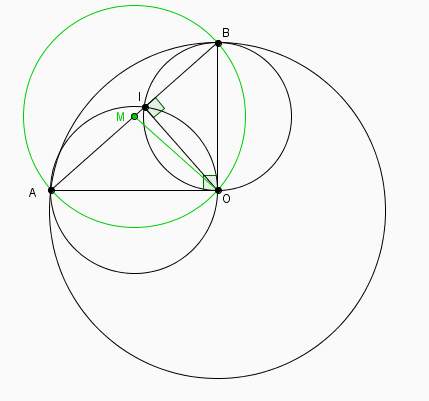
Tracer un cercle de centre O et de rayon 4 cm, puis marquer deux point A et B du cercles tels que (OA) et (OB) soient perpendiculaires. Tracer les cercles de diamètre (OA) et (OB). On appelle I leur deuxième point d'intersection.
1° Prouver que les triangle IOA et IOB sont rectangles en I
2° En déduire au A, I, B sont alignés
3° Prouver que I est le milieu de (AB)
J'ai fait le dessin, mais pour le 1° mes triangles sont rectangles en A et B. Donc tout le reste ne vas pas non plus. Il ne sont pas alignés et I n'est donc pas le milieu.
J'ai refait plusieurs fois le dessin mais j'arrive toujours à la même chose.
Quelqu'un peut-il m'aider ? Merci
Bonjour
maximelillois
Citation :
J'ai fait le dessin, mais pour le 1° mes triangles sont rectangles en A et B. Donc tout le reste ne vas pas non plus. Il ne sont pas alignés et I n'est donc pas le milieu.
J'ai fait le dessin, mais pour le 1° mes triangles sont rectangles en A et B. Donc tout le reste ne vas pas non plus. Il ne sont pas alignés et I n'est donc pas le milieu.
Ton dessin doit être faux
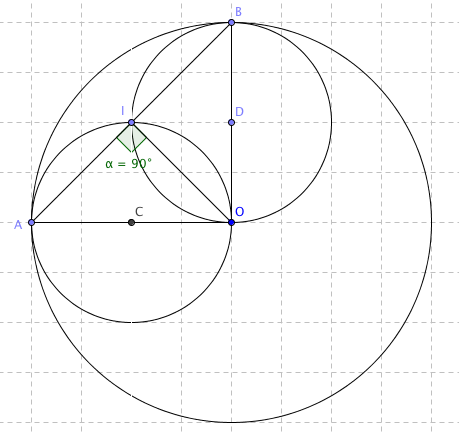
merci beaucoup MIJO, en effet mon dessin était faux. J'avais pris le rayon de (AO) et (BO) et non pas le diamètre.
Ça va aller beaucoup mieux.
Encore merci
re-bonjour,
j'ai répondu au 1° et 2° mais pour le 3°, j'ai un soucis, je n'arrive pas à trouver la propriété. Pourriez-vous m'aider. Merci
3)
On regarde le dessin , le grand cercle de rayon 4 cm
et on voit : OA = OB = le rayon .
AOB est un triangle isocèle en O
OA = OB
[OI] est la hauteur issue de O
mais dans un iso ,
c' est aussi : une médiane , une bissectrice et la médiatrice de [AB]
Merci LAJE,
voilà ce que moi j'ai répondu :
Dans le triangle ABO, on sait que (AO) est [sub][/sub
(BO) donc le triangle ABO est rectangle en O.
Dans un triangle rectangle, le centre du cercle circonscrit est le milieu de l'hypoténuse.
Donc I est le milieu de (AB)
Qu'est-ce que tu en penses et qu'en pensez-vous tous ?
merci
Cela part sur de bonnes intentions ,
mais il n' y a pas de cercle circonscrit au triangle rectangle ABO