Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale IntégrationTopics traitant de Intégration [tout]Lister tous les topics de mathématiques
Niveau terminale
Partager :

Coefficient de Gini

Posté par
Luca75 26-02-12 à 10:42

Bonjour, j'essaie de faire des exercices pour m'entrainer pour le bac et je bloque sur un exercice. Voici l'énoncé :
On considère la fonction f définie sur [0;1] par f(x)=x^3-0.5x²+0.5x. La courbe Cf fournie une approche acceptable de la courbe de concentration du revenu.

1. Calculer les images de 0, 1 et 0.5 !
Donc, je trouve f(0)=0 ; f(1)=1 ; f(0.5)=0.25


2. Calculer le coefficient de Gini du revenu obtenu à l'aide de cette fonction.
Et là, je ne sais pas comment faire. Je sais que c'est égal à l'aire de concentration sur l'aire du triangle AOB inscrit dans un repère sachant que l'origine du repère est appelée O, que ce triangle est rectangle en A (qui a pour coordonées (1;0)) et a pour longueur 1 (axe des abscisses) et hauteur 1 (en ordonnée) ! Je ne sais pas si je suis très clair...

Donc, pour moi, l'aire du triangle est 0.5 car (1x1)/2=0.5
et après, je ne sais pas comment calculer l'aire de concentration sachant que celle-ci est la partie entre la courbe Cf sur [0;1] et la base du triangle d'équation y=x !

Voilà, je ne sais pas faire de repère, ni de courbe sur ce forum, donc j'ai essayé de vous expliquer comme je pouvais. En espérant que vous pourrez comprendre les informations données et que vous pourrez m'aider au plus vite.

Merci !

Posté par
yogodore : Coefficient de Gini 26-02-12 à 10:50

Bonjour

Si j'ai bien compris ce que tu as expliqué il faut calculer l'aire qui est entre la courbe f et la droite d'équation y=x donc il faudrait que tu calcules :

\int_{0}^{1}f(x)dx-\int_{0}^{1}xdx

Mais c'est à revérifier...

Posté par
Luca75re : Coefficient de Gini 26-02-12 à 11:10

Ouiii, c'est ça ! Ahh, j'avais peur de m'être mal exprimé !

Donc, je fais la primitive de f qui est
F = (x^4/4) -0.5 x (x^3/3) + 0.5 x (x²/2)
F(1)-F(0)
4/12 - 0 = 4/12

Et, la primitive de x est x²/2
Donc, F(1)-F(0)
1/2-0=1/2

Ainsi, 4/12 - 1/2 = -1/6
Donc, l'aire de concentration est de -1/6 (je trouve bizard de trouver un résultat négatif...)

Le coefficient de Gini est donc : (-1/6)/(1/2)=-1/3
Je dois m'être trompé, mais je ne vois pas où.
Merci de votre aide !

Posté par
yogodore : Coefficient de Gini 26-02-12 à 11:24

Je ne sais pas si c'est normal de trouver un coefficient de Gini néfatif mais graphiquement c'est logique puisque la courbe f est en dessous de la droite d'équation y=x (cf figure)

Par contre je ne trouve pas \frac{4}{12} pour F(1)-F(0), je trouve \frac{5}{12}

F(x)=\frac{x^4}{4}-\frac{1}{2}*\frac{x^3}{3}+\frac{1}{2}*\frac{x²}{2}=\frac{x^4}{4}-\frac{x^3}{6}+\frac{x²}{4}

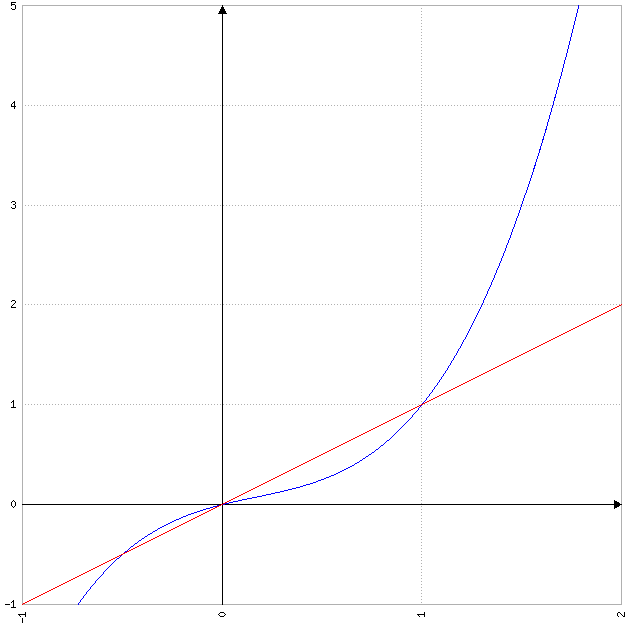
Coefficient de Gini

Posté par
yogodore : Coefficient de Gini 26-02-12 à 11:25

Ah non tu as raison désolé le résultat que tu as trouvé est correct

Posté par
yogodore : Coefficient de Gini 26-02-12 à 11:30

Je viens de faire des recherches sur le coefficient de Gini et en fait il faut prendre 2 fois l'aire en verte sur la figure. Si on note k le coefficient de Gini alors puisque f(x)-x<0 sur [0;1] on a :

k=2(\int_{0}^{1}xdx-\int_{0}^{1}f(x)dx)=2\frac{1}{3}=\frac{2}{3}

Et là c'est plus cohérent puisque le coefficient de gini est compris entre 0 et 1

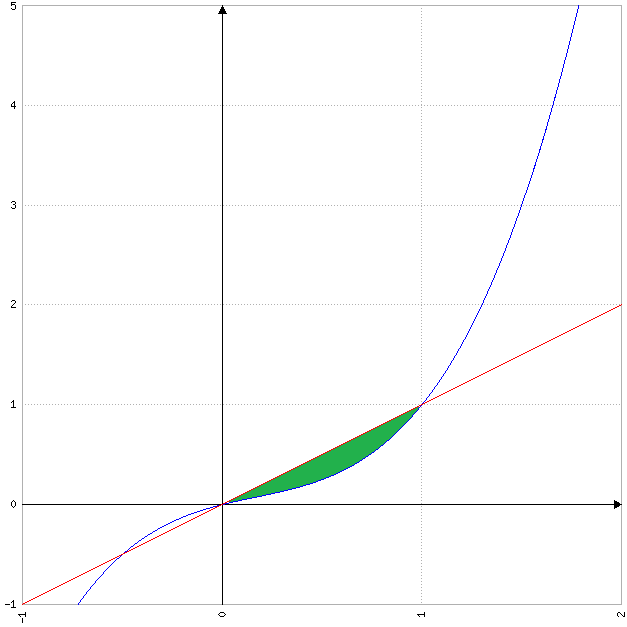
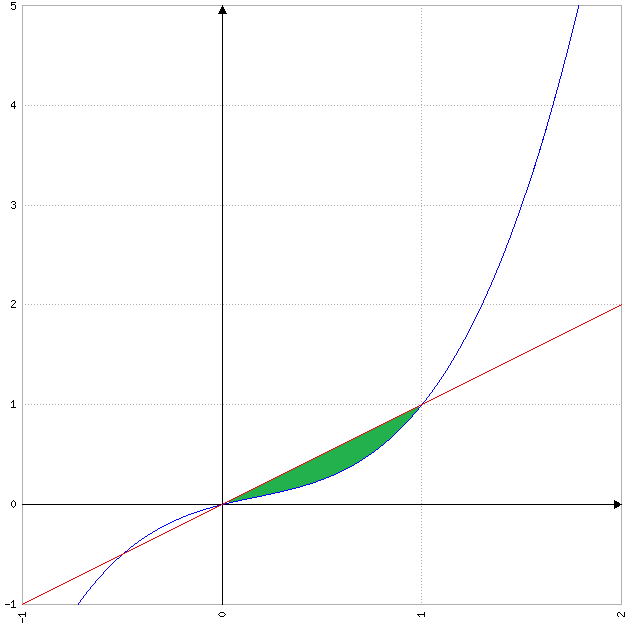
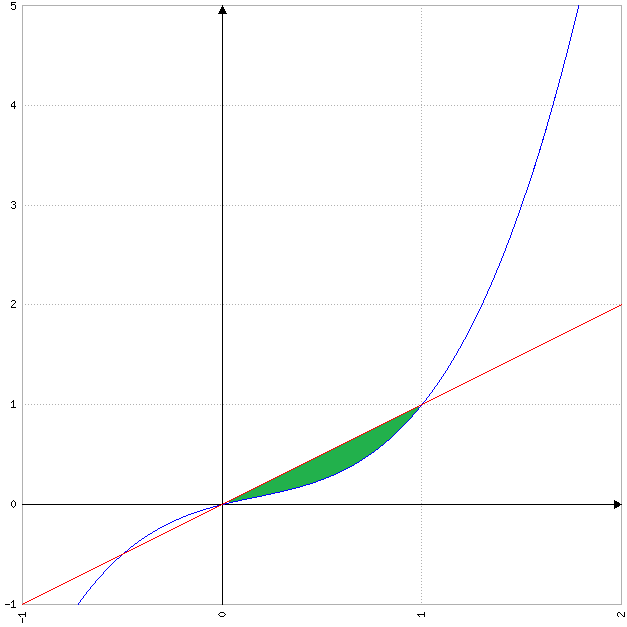
Coefficient de Gini

Coefficient de Gini

Coefficient de Gini

Posté par
Luca75re : Coefficient de Gini 26-02-12 à 11:34

Merci, avec le repère, il est plus facile de se représenter les choses !

Mais, dans mon énoncé, on me dit que le coefficient de Gini est compris entre 0 et 1 ! Et que si il est égal à zéro la répartition est parfaitement égalitaire et si il est égal à 1 la répartition est inégalitaire...

Peut-être qu'il faudrait inversé, c'est à dire faire Sxdx-Sf(x)dx , non ?

Donc, 1/2 - 1/12 =1/6
Le coefficient de Gini serrait donc de 1/6, ce qui reviendrait à dire que la répartition est presque égalitaire !

Qu'est ce que vous en pensé ?

Posté par
Luca75re : Coefficient de Gini 26-02-12 à 11:35

Ahh, j'ai posté sans lire votre réponse d'avant ... je regarde !

Posté par
yogodore : Coefficient de Gini 26-02-12 à 11:38

Je me suis trompé dans le résultat tu dois trouver k=2*\frac{1}{6}=\frac{1}{3}

Posté par
Luca75re : Coefficient de Gini 26-02-12 à 11:44

Je ne comprend pas pourquoi il faut multiplier par 2 car si on fait
Aire de concentration = Sxdx -Sf(x)dx : on trouve 1/6
Donc, le coefficient de gini serrait : (1/6)/(1/2)=1/3

Et, ainsi on ne trouverait pas un résultat négatif, non ?

Posté par
yogodore : Coefficient de Gini 26-02-12 à 11:52

D'après ce que j'ai vu sur internet, le coefficient de Gini c'est deux fois l'aire entre la courbe et la droite d'équation y=x. Ici comme la courbe est en dessous de la droite, il faut calculer \int_{0}^{1}xdx-\int_{0}^{1}f(x)dx, pour pouvoir avoir quelque chose de positif (car le coefficient de gini est positif)

Posté par
Luca75re : Coefficient de Gini 26-02-12 à 12:05

D'accord ! Je vous remercie pour vos recherches !
Pour autant, dans mon exercice du livre on me dit de calculer ce coefficient en faisant seulement : aire de concentration sur aire du triangle OAB. Donc, je vais respecter cette démarche...
Ce qui revient a dire :
Aire de concentration = Sxdx -Sf(x)dx=1/6
Et, vu que l'aire du triangle OAB est 1/2
Le coefficient de Gini est : (1/6)/(1/2)=1/3

Donc, au final, on trouve le même résultat à savoir 1/3 sans avoir fait la même démarche !

Et ce que mon développement est juste si on part de la méthode du livre ?
Merci beaucoup !

Posté par
yogodore : Coefficient de Gini 26-02-12 à 12:10

Non ce n'est pas correct ce que tu appelles aire de concentration c'est juste \int_{0}^{1}f(x)dx graphiquement c'est l'aire sous la courbe.

Posté par
Luca75re : Coefficient de Gini 26-02-12 à 12:24

Je ne comprend pas, au début vous m'avez dit : "il faut calculer l'aire qui est entre la courbe f et la droite d'équation y=x donc il faudrait que tu calcules : Sxdx-Sf(x)dx" pour trouver l'aire de concentration.

Bon, je recommance avec ce que vous venez de me dire et (avec la méthode du livre) :
Aire de concentration=Sf(x)dx=F(1)-F(0)=4/12=1/3
et on sait que l'aire du triangle est 1/2
Donc, coefficient de Gini=(1/3)/(1/2)= 2/3

Le coefficient de Gini est donc de 2/3. Est-ce que ça va mieux ?
Merci.

Posté par
yogodore : Coefficient de Gini 26-02-12 à 12:35

Je reprends tout depuis le début (je n'ai pas été très clair je l'avoue)

aire de concentration : \int_{0}^{1}f(x)dx=F(1)-F(0)=\frac{4}{12}

aire du triangle : \int_{0}^{1}xdx=\frac{1}{2}

On voit que l'aire du triangle est plus grande que l'aire de concentration donc pour que le coefficient de Gini respecte la positivité il faut faire k=aire di triangle-aire de concentration soit : k=\frac{1}{2}-\frac{4}{12}=\frac{1}{6}

Voila ton coefficient de Gini.

Bon normalement d'après ce que j'ai lu sur internet le coefficient réel correspond à deux fois cet aire mais si ils ne te parlent pas de ceci tu laisse k=\frac{1}{6}


Est-ce plus clair maintenant?

Posté par
Luca75re : Coefficient de Gini 26-02-12 à 12:46

J' ai bien compris l'aire de concentration et l'aire du triangle !

Mais pourquoi faut-il faire une soustraction entre l'aire du triangle et l'aire de concentration ?

Car encore selon mon livre, c'est : Aire de concentration SUR Aire du triangle et cela donnerait un résultat positif aussi.  

Merci beaucoup pour votre patience, c'est très gentil !

Posté par
yogodore : Coefficient de Gini 26-02-12 à 13:13

ah c'est la division et non la soustraction !!!!!!

Ok j'étais complêtement à côté

Dans ce cas oui ça donnera :

\frac{\frac{4}{12}}{\frac{1}{2}}=\frac{2}{3}

Sauf erreur de ma part...

Posté par
Luca75re : Coefficient de Gini 26-02-12 à 13:23

Ok, super !!! Je suis content d'avoir compris ! Merci beaucoup pour toutes vos recherches et surtout votre patience !
A bientôt, peut-être !

Posté par
yogodore : Coefficient de Gini 26-02-12 à 13:32

De rien

Et je n'espère pas à bientôt ça signifiera que tu n'as plus besoin d'aide en maths

Posté par
Luca75re : Coefficient de Gini 26-02-12 à 18:14

Je crois que c'est faut, je m'explique :

Je calcul l'aire de concentration qui est la partie verte des graphiques précédents :
C'est : l'aire du triangle - l'aire de la partie sous la courbe
Or, l'aire du triangle est 1/2 et l'aire de la partie sous la courbe est Sf(x)dx qui est 2/6
Donc : 1/2 - 2/6 = 1/6

Par conséquent, on sait que le coefficient de Gini est : aire de concentration SUR aire du triangle OAB
Donc : (1/6)/(1/2) = (1/6) x 2 = 1/3

Le coefficient de Gini est donc de 1/3 !!! Est ce qui serrait possible que vous vérifiez ma démarche ? Merci !

Posté par
Luca75re : Coefficient de Gini 27-02-12 à 13:03

Est-ce qu'il serrait possible que quelqu'un me réponde ?

Posté par
Luca75re : Coefficient de Gini 27-02-12 à 15:28

?? S'il vous plait !

Posté par
Luca75re : Coefficient de Gini 27-02-12 à 16:23

Quelqu'un pourrait m'aider et me répondre ? Ca serrait sympa !

Posté par
Luca75re : Coefficient de Gini 27-02-12 à 16:50

Je ne comprend pas pourquoi personne ne me répond... ça fait depuis qu'il est 13h que j'attend une réponse...

Et, une autre question : quelle est la primitive de 3x/(x²+2)² ?
Je dirais : (1/2)(2x/(x²+2)) mais je ne suis vraiment pas sûr !

Merci d'avance !

Posté par
Luca75re : Coefficient de Gini 27-02-12 à 17:57

...

Posté par
Luca75re : Coefficient de Gini 27-02-12 à 18:20

...

Posté par
Luca75Indice de gini 27-02-12 à 18:31

Re-bonjour

Personne ne me répond depuis qu'il est 13h sur mon autre topic, donc je me vois dans l'obligation d'en créer un nouveau (Désolé)

C'est le même exercice que mon topic d'avance et je crois que ce que nous avons conclu est faux, je m'explique :

Je calcule l'aire de concentration qui est la partie verte des graphiques précédents :
C'est : l'aire du triangle - l'aire de la partie sous la courbe
Or, l'aire du triangle est 1/2 et l'aire de la partie sous la courbe est Sf(x)dx qui est 2/6
Donc : 1/2 - 2/6 = 1/6

Par conséquent, on sait que le coefficient de Gini est : aire de concentration SUR aire du triangle OAB
Donc : (1/6)/(1/2) = (1/6) x 2 = 1/3

Le coefficient de Gini est donc de 1/3 ! Est ce qui serrait possible que vous vérifiez ma démarche ? Merci

*** message déplacé ***

Posté par
Luca75re : Coefficient de Gini 28-02-12 à 20:53

...

Posté par
veledare : Coefficient de Gini 29-02-12 à 08:57

bonjour,
je n'ai pas suivi depuis le début mais ce que tu écris dans ton dernier post est correct l'indice de gini est bien égal à \frac{1}{3}
tu peux aussi retenir que l'indice de gini c'est l'aire du carré de côté 1-2fois l'aire de la partie sous la courbe soit 1-\frac{2}{3}=\frac{1}{3}

Posté par
Luca75re : Coefficient de Gini 29-02-12 à 13:26

Ahh ! Enfin, une réponse !! Merci beaucoup !
Et, vers la fin de mon exercice on me demande de trouver la primitive de
x/(x²+2)² ! Je dirais : -1/(x²+2)

Est-ce que vous pourriez me dire si c'est bon ou pas ?
Merci

Posté par
Luca75re : Coefficient de Gini 29-02-12 à 14:42

...

Posté par
veledare : Coefficient de Gini 29-02-12 à 17:40

une bonne methode pour savoir si c'est exact :tu dérives \frac{-1}{x^2+1}
et tu vas t'apercevoir que ce n'est pas tout à fait cela

Posté par
Luca75re : Coefficient de Gini 29-02-12 à 18:14

Ahh ! Heu, je cherche la primitive de x/(x²+2)²... Donc c'est : -x/(x²+2)
Et, c'est pareil, la primitive de x/(x²+1) est : -x/(x²+1)

Est-ce que c'est correct ? Et, si oui, je ne comprend pas ces histoires de remise à égalité au niveau des primitives. Comment sait-on qu'il faut rajouter un nombre devant la primitive ?

Posté par
veledare : Coefficient de Gini 29-02-12 à 19:53

non,
d'abord tu trouves une primitive pas la primitive
si tu dérives \frac{-1}{x^2+2} tu obtiens \frac{2x}{(x^2+2)^2} donc ce n'est pas tout à fait cela ,il faut diviser par 2
une primitive de \frac{x}{(x^2+2)^2} c'est\frac{-1}{2(x^2+2)}

Posté par
veledare : Coefficient de Gini 29-02-12 à 20:08

quand tu as une primitie F d'une fonction f toute primitive H de f est de la forme H=F+C avec C constante
on peut te demander de trouver la constante C pour que H prenne la valeur a pour x=x0tu écrisH(x_0)=F(x_0)+C=a=>C=a-F(x_0)
c"est cela que tu ne comprenais pas ou bien c'est autre chose

Posté par
Luca75re : Coefficient de Gini 29-02-12 à 20:18

Merci pour votre aide !
Okay, donc par exemple : une primitive de x/(x²+1)² est -1/(2(x²+1))

Est-ce que j'ai bien compris ?

Posté par
veledare : Coefficient de Gini 29-02-12 à 21:38

oui
et si tu cherches  laprimitive nulle pour x=1 par exemple tu écris que H(1)=0 donc F(1)+C=0 d'où C=-F(1) ce qui donne dans le cas de ton exercice C=\frac{1}{6}

Posté par
Luca75re : Coefficient de Gini 01-03-12 à 16:11

Okay et pour F(x)=-1/(2(x²+1)), on aurait C=-F(1), donc C=1/(2(x²+1))
Ce qui donnerait : C=1/4

Et pour C=-F(0) avec F(x)=-1/(2(x²+1)), on aurait C=1/(2(0²+1))
Ce qui donnerait : C=1/2

Je vous soumets quelques exemples pour voir si j'ai bien compris !
Merci !

Posté par
veledare : Coefficient de Gini 01-03-12 à 17:54

oui dans le premier cas c'est bien 1/4 par étourderie j'ai mis 1/6
tu as compris


Rechercher
Menu
Espace membre
8 visiteurs
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1742 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !