Niveau terminale

Complexes / Ensemble de points

Posté par
Keren 15-03-16 à 19:51

Bonsoir , pourriez vous m'aider sur cet exercice ?

$A(a=-2i) , B(b=\sqrt{3}-i), C(c=2ie^{i\theta })$ / $\theta \in \left ] \frac{-\pi }{2};\frac{\pi }{2} \right [$

* Calculer $Z = \frac{c-a}{b-a}$
- Je trouve que $Z= -4sin(\frac{\theta }{2})e^{i\theta }$ lorsque $\theta \in \left ] 0;\frac{\pi }{2} \right [$

et que $Z = 4sin(\frac{\theta }{2})e^{i(\frac{\theta }{2}+\pi )}$ lorsque $\theta \in \left ] \frac{-\pi }{2};0 \right [$

--> Définir l'ensemble des points $M(Z)$ lorsque $\theta$ varie sur $\left ] \frac{-\pi }{2};\frac{\pi }{2} \right [$

Merci

Posté par re : Complexes / Ensemble de points 15-03-16 à 20:00

Bonjour,

Pourquoi faire des calculs differents selon l'intervalle dans lequel est ?

Posté par re : Complexes / Ensemble de points 15-03-16 à 20:02

On me demande de l'écrire sous sa forme exponentielle

Posté par re : Complexes / Ensemble de points 15-03-16 à 20:23

Oui, et alors?

Posté par re : Complexes / Ensemble de points 15-03-16 à 20:24

- Le module doit être positif

Posté par re : Complexes / Ensemble de points 15-03-16 à 20:56

Je n'ai pas essayé d'arriver à ton résultat qui me surprend un peu, mais je trouve que la forme $e^{i\frac{\pi }{3}}(e^{i\theta }+1)$ plus adaptée à la suite de l'exercice.

Posté par re : Complexes / Ensemble de points 16-03-16 à 10:54

Bonjour,

Citation :
- Je trouve que $Z= -4sin(\frac{\theta }{2})e^{i\theta }$ lorsque $\theta \in \left ] 0;\frac{\pi }{2} \right [$

et que $Z = 4sin(\frac{\theta }{2})e^{i(\frac{\theta }{2}+\pi )}$ lorsque $\theta \in \left ] \frac{-\pi }{2};0 \right [$

Ce résultat n' est pas bon:

  Sous forme exponentielle: $z=2\,\cos\,\dfrac{\theta}{2}\,e^{i\left(\frac{\theta}{2}+\frac{\pi}{3}\right)}$ (1)

Au reste sanantonio312 n' a pas tort; un demi cercle de centre $O$ , de diamètre $[JK]$ et de rayon 1, une translation de vecteur $\vec{u}$ suivi d' une rotation $(0,\frac{\pi}{3})$ et l' affaire est dans le sac. (les demi cercles en noir sur la figure).

Sinon, à partir de (1), tu as plusieurs possibilités:

  -Soit passer en coordonnées cartésiennes:

       $\begin{cases}X_C=2\,\cos\,\dfrac{\theta}{2}\,\cos\,\left(\dfrac{\theta}{2}+\dfrac{\pi}{3}\right)\\Y_C=2\,\cos\,\dfrac{\theta}{2}\,\sin\,\left(\dfrac{\theta}{2}+\dfrac{\pi}{3}\right)\end{cases}$

   et vérifier que $\left(X_C-\dfrac{1}{2}\right)^2+\left(Y_C-\dfrac{\sqrt{3}}{2}\right)^2=1$ en justifiant que $C$ ne décrit qu' une partie de ce cercle lorsque $\theta \in\left]-\dfrac{\pi}{2};\dfrac{\pi}{2}\right[$

  -Soit si tu connais les courbes en polaire:

      On pose $\varphi=\dfrac{\theta}{2}+\dfrac{\pi}{3}$

      d' où $\theta =2\varphi -\dfrac{2\pi}{3}$

      et l' équation en polaire du lieu de $C$ :

       $\rho=2\,\cos\,\left(\varphi -\dfrac{\pi}{3}\right)$ avec $\varphi\in\left]\dfrac{\pi}{12};\dfrac{7\pi}{12}\right[$

Il existe d' autres voies, par exemple:

$c=2\,ie^{i\theta}=2\,e^{i(\theta+\frac{\pi}{2})}$

$\theta +\dfrac{\pi}{2}\in]0,\pi[$ et $C$ décrit le demi cercle de rayon 2 de diamètre $[DE]$ (en bleu sur la figure)

$z=\dfrac{1}{b-a}\,c-\dfrac{a}{b-a}$

$z=\dfrac{1}{2}\,e^{-\frac{i\pi}{6}}c+\dfrac{1+i\sqrt{3}}{2}$

$Z$ est l' image de $C$ dans la similitude $S$ de rapport $\dfrac{1}{2}$ , d' angle $-\dfrac{\pi}{6}$ et de centre $\Omega$ construit sur la figure mais dont on se moque pour ton problème.

$S(O)=O'$ avec $o'=\dfrac{1+i\sqrt{3}}{2}=e^{\frac{i\pi}{3}}$

Le lieu de $Z$ est donc le demi cercle de centre $O'$ et de rayon $1$ en sorte que son diamètre $[D'E']$ soit tel que $(\vec{DE};\vec{D'E'})=-\dfrac{\pi}{6}\;\;[2\pi]$

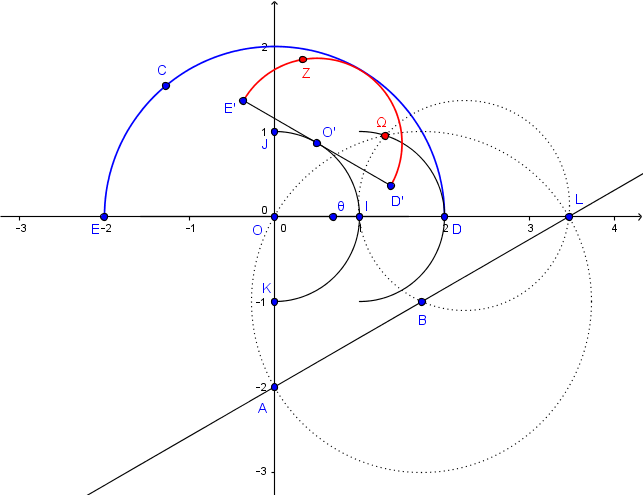
Complexes / Ensemble de points

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de maths

Nombres complexes en terminale
9 fiches de mathématiques sur "nombres complexes" en terminale disponibles.

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

Cours et Exercices de maths

Forum de maths

college

lycee

Outils de maths

Pages les plus populaires

Complexes / Ensemble de points

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de maths