Inscription / Connexion Nouveau Sujet
composée de deux isométries
salut,
Soit ABC un triangle équilatéral de sens direct . On désigne I milieu de et J milieu de
et par O le centre du cercle circonscrit au triangle ABC .Soient E et F les points diamétralement opposes respectivement a A et C
On considéré l'isométrie f du plan transformant A en E et O en B.
1)a) Montrer que J est le milieu de puis déterminer E'=f(E)
b) Montrer que les points A,F,E' sont alignés , en déduire que F est le milieu de
.
2)a) On pose g=to f . Déterminer g(A), g(O),g(E)
(respectivement C,O,F)
b)En déduire que f est la composée d'une translation et d'une rotation ou bien d'une
translation et d'une symétrie axiale.
c) Caractériser f dans chacun de ces deux cas.
je peine à résoudre la question 2)b).
Merci d'avance.
bonjour
moi déjà j'ai un problème avec l'énoncé...
On considéréL'isométrie f du plan transformant A en E et O en B.
cet article défini me semble abusif !
et puis la question 2b est curieuse également... toute isométrie du plan est sous cette forme !
soit l'énoncé est mal recopié, soit il est bizarre !
Bonjour,
Avant de répondre à 2)b), il faut caractériser
L'as tu fait ?
rotation ou bien symétrie centrale ? car elle fixe un point .
Pour l'énoncé : j'ai vérifié.
La figure:
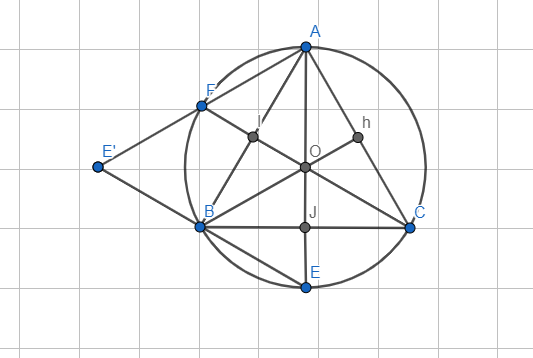
rotation ou bien symétrie centrale ? car elle fixe un point .
Rotation, oui ou symétrie axiale.
Les remarques de matheuxmatou sont parfaitement justifiées. Ton énoncé est un peu olé olé...
Je t'invite à regarder cette figure avec attention :
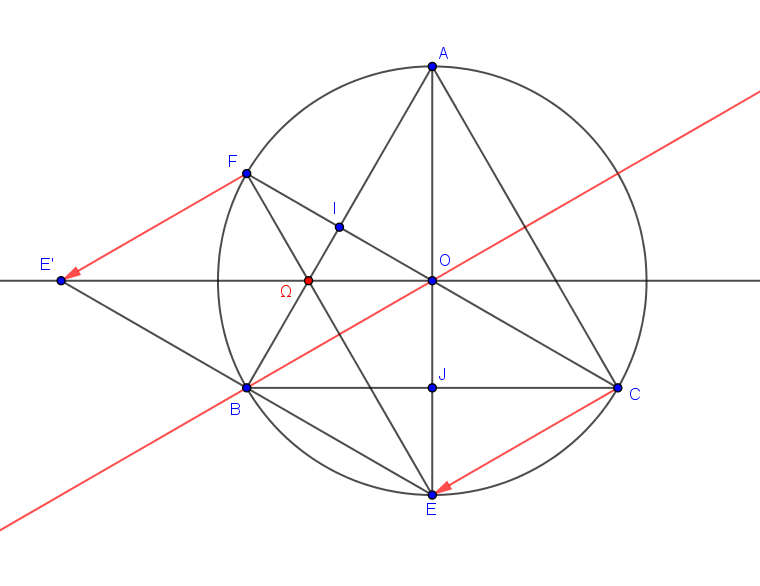
Et en tirer les conclusions :
Je vois au final une rotation et une symétrie glissée ...
La rotation est plutôt de centre et d'angle
Je t'ai indiqué le résultat avec une figure. C'était une indication comme une autre.
Il reste à déterminer comment y parvenir. Autrement dit : tout reste à faire.



