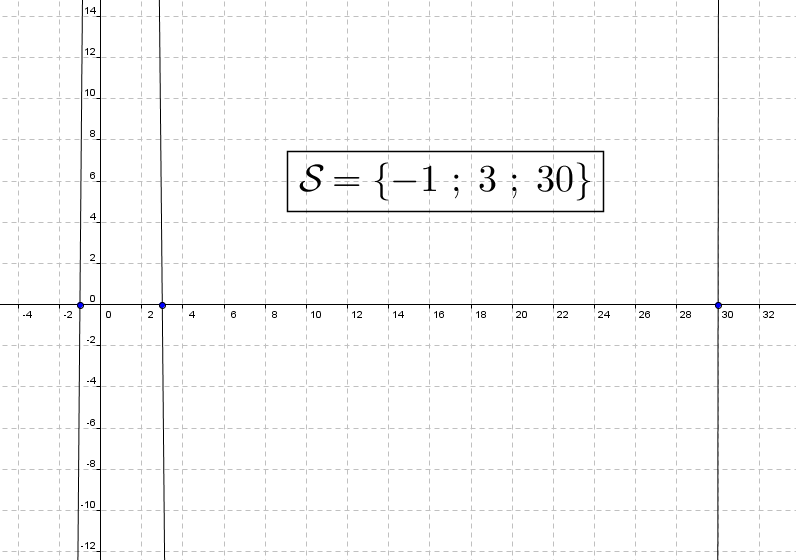Bonsoir lola470 !
Quelle calculatrice as-tu ? J'ai une TI-83 Plus.fr.

bonsoir
tracez la courbe représentative de votre fonction et regardez les intersections avec l'axe des abscisses

Bonjour hekla (beau pseudonyme emprunté au nom du volcan islandais, je présume) !
Tout à fait !

pour Jay-M tout à fait

Oui j'ai un TI 83 Plus.fr

Merci mais pour tracer la courbe il faut entrer l'equation ds la calculette non?

Recopie le membre de gauche de l'équation dans « \Y₁ = » après avoir appuyé sur « f(x) ».

Donc je met pas =0?

Non, parce que comme l'a dit hekla, il suffit ensuite de repérer les abscisses des points d'intersection avec l'axe des abscisses.

donc je rentre  ma fonction mais quand je tape f(x) sa fait rien
meme quand je met graphe je voie que l'axe mais pas la courbe

Oh non, encore un problème...
Es-tu sûr(e) que tu n'as pas commis d'erreur(s) en tapant l'expression ?

Beeh je pence pas.
Est-ce qu'il faut regler xmin, xmax...?

Ah oui, très bien, tu as trouvé la solution au problème ; modifie notamment « Xmax » étant donné que 30 est une solution de l'équation (tiens, je viens de répondre à la question 2 au passage ).

bien sûr
xmin -5
xmax 5
xscl 1
Ymin -10
ymax 100
Yscl 20

on peut le faire après  les solutions sont entières

Pfiouuuu sa me met Err: window range

Ah c'est bon j'ai une courbe

Elle passe par -1 et par 3

D'accord...
Bon, je te montre mon graphique réalisé à partir de GeoGebra :

Oui j'ai pareille sauf que je voi pas le 30 moi c"est trop petit

C'est normal, tu n'a pas changé « Xmax » ; transforme-le en « 50 » par exemple.

et le xmin en 25

ah oui c'est bon.
derniere question et je vous laisse trkl!
donné l'encadrement d'empliude 10 puissance -3

Je ne sais pas quoi répondre à cette question, désolé, je n'ai jamais vu cela en cours !
Mais hekla pourra t'aider !

D'acord pas de problème!
En tout cas merci beaucoup

je veux bien aider mais donner l'encadrement de quoi à
si ce sont des solutions de l'équation  elles sont exactes