Inscription / Connexion Nouveau Sujet
construction d'une parabole
bonjour à tous avec le logiciel geogebra , on place le point A(0;2)
a partir d'un point B de l'axe des abscisses,on construit le point D1 à l'intersection de la médiatrice du segment AB et parrallele à l'axe des ordonnées passant par B en decochant afficher objet on garde visible que les points A et D
1) reproduire 5 fois cette construction sur le même dessin en changeant les points des abscisses .On nommerqa les points D1 D2 D3 D4 D5 les points ainsi construits.
2)faire construire une courbe passant par les points D1 D2 D3 D4 D5
lire alors dans la fenêtre algebre l'équation de cette courbe
3) vérifier que cette equation peut se mettre sous la forme y=f(x)ou x petite barre flêche 1/4 x²+1
4) on se propose maintenant de démontrer que tout point construit sur le modèle D1 est sur la courbe répresentative de f . on considère donc un point B (a;0) quelconque de l'axe des abscisses . Que peut on dire de l'abscisse du point que l'on veut construire ?
calculer alors l'ordonnée b et D en fonction de a et conclure .
j'ai besoin d'aide svp pour cette exercice je bloque totalement & surtout pour la construction ! mercii
Bonjour,
voilà un exemple de construction avec un point B1 d'où D1
et c'est ça que tu dois refaire plusieurs fois !
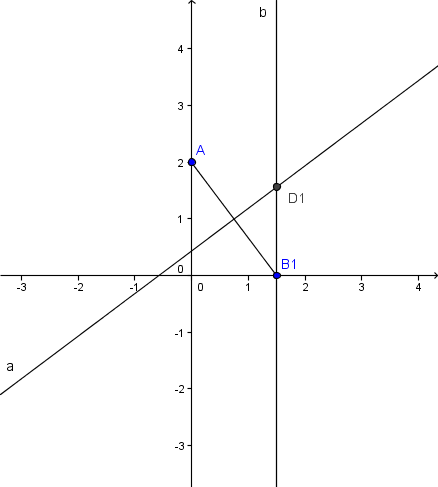
tu places dans la barre de saisie A=(0,2)
ensuite tu choisis B1 sur l'axe des abscisses
tu traces la médiatrice de AB1
et la parallèle à l'axe des ordonnées passant par B1
ces deux droites se coupent en D1
tu prends B2
et tu recommences....
dans le menu des droites perpendiculaires, tu as aussi parallèle à
tu choisis le point B1 puis l'axe des y
et ça te trace la //
et j'ai reussi merci & apres on me demande de refaire le meme 5 fois je le fais sur un nouveau quadrillage ou sur le même && je prends n'importe quel abscisse
tu le fais surtout sur le même dessin, en prenant effectivement n'importe quelle abscisse, positive ou négative....
ordonnée je prends le meme c'est a dire 2
je ne comprends pas ce que tu demandes, désolée....
tu choisis le menu à côté des cercles
il y a conique passant par 5 points
et tu cliques sur tes 5 points
ça va te tracer ta parabole....magique !
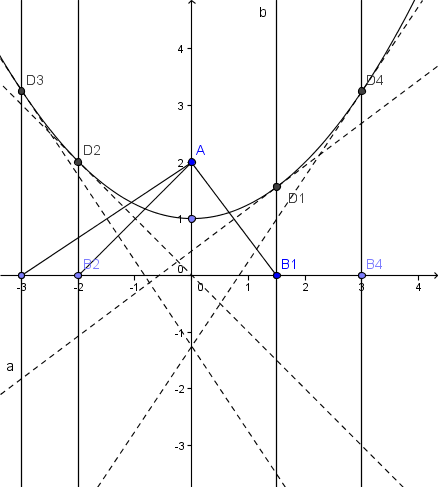
tu fais afficher (affichage, fenêtre algèbre)
et à gauche, normalement, en bas, l'équation de ta courbe s'est écrite....
encore magique !

je vais m'arrêter pour ce soir..
je viendrai voir demain si tu as eu d'autres questions...
fais bien attention à ta molette!....
Bonjour !
je m'excuse tout d'abord de re-lancer ce topic sur cet exercice mais je cherche actuellement la réponse à la question 4. Afin de comprendre ce que je dis, il est plus facile de relire l'énoncé de l'exercice se trouvant dans le premier post.
J'ai trouvé que l'abscisse de B est la même que celle de D, et j'ai également trouvé un éventuel résultat pour b (l'ordonnée du point D) mais que dans le cas où B et C sont confondus (C étant le milieu de [AB], mais cela ne démontre donc pas pour le cas général).
De plus, le but de la question étant de prouver que tout point créé sur le même modèle que D1, appartient à la parabole).

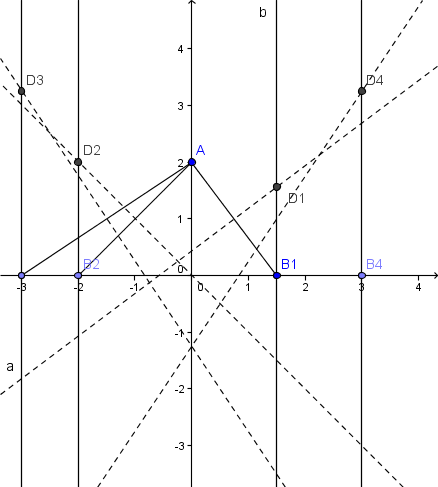
 !
!