Inscription / Connexion Nouveau Sujet
construire un arbre
voila comme le dit dans le titre il faut que je construire n arbre le seul probleme c'est je n'y arrive pas a faire toutes les possibilites je n'arrête de me planter.
on dispose un quadrillage avec un chemin de A vers B est une suite de 6 deplacement 3 vers le haut (H) et 3 vers la droite (D) dans n'importe quel ordre
dans l'image c'est H,D,H,D,D,H est un chemin de A vers B
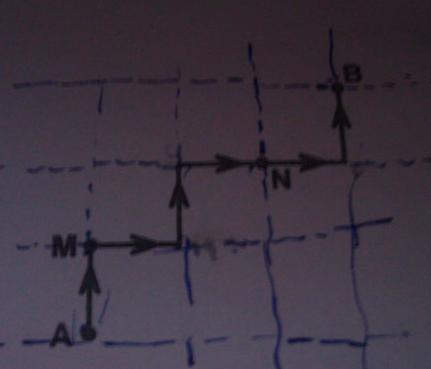
il suffit de le voir comme ca:
tu as 6 déplacements a faire, 3 vers le haut (H) et trois vers la droite (D).
C'est comme si tu avais 6 cases à remplir, avec 3 H et 3D.
Si tu choisis ou mettre les H (ca c'est choisir 3 parmi 6 sans arrangements) donc C(6,3)
le reste c'est forcement les D.
Donc il y a C(6,3) chemins.
salut
il y a 6 deplacements du type i,i,i,j,j,j ( vecteurs unitaires du repère (A,i,j)) (donnés ici dans un ordre quelconque)!
si on cherche tout les combinaisons possibles de la suite i,i,i,j,j,j il suffit de rechercher toutes les places possibles
de i ou de j , pour i on a donc C6,3 =6!/3!.3!=20 combinaisons possibles
Ce que je comprend pas c'est le calcule et qu'aprés on me demande quelle la probabilité qu'il passe par le point M
tu as 20 chemins possibles.
Calcule le nombre de chemin qui passent par M. (indice: ca veut dire que dans le scase, on met un H en premier, il reste a compter les solutions posibles pour la suite, ou mettre les 2 H qui restenht parmi 5 case restantes)
En faisant le rapport, tu aura ta proba.
de A vers M une seule facon d'y aller : selon j
de M vers B 2 deplacements selon j et 3 deplacements selon i
soit j,j,i,i,i il suffit de trouver toutes les postions possibles de j dans cette suite
5 deplacements et donc manière de prendre 2 places parmi 5 ou 3 places parmi 5 ( c'est pareil )
on calcul donc C5,2=10 soit aussi la valeur de C5,3 soit en tout 1 facon d'aller de A vers M fois le nbr de facons d'aller
de M vers B soit 1.10=10 et P=10/20=1/2
et donc P=10/20=1/2


