Inscription / Connexion Nouveau Sujet
construite une section de cube
Bonjour,
Pouvez vous m'aider pour cet exercice.
Voici l'enoncé :
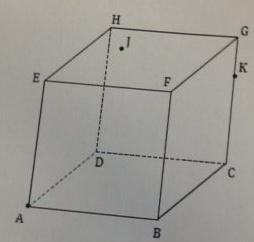
Construire la section du cube par le plan (AJK) lorsque l le point J appartient au plan (EFH) .
Vous pourrez d'abord utiliser le plan (AEJ) pour tracer l'intersection de la droite (AJ) et du plan (DCH).
Vous laisserez apparents vos traits de construction pour justifier votre réponse.
La figure en piéce jointe (désolé je n'ai pas réussi à la faire pivoter)
Merci d'avance
Bonjour,
les intersections c'est toujours du simple bon sens (dans quel plan ce trouve telle droite etc)
intersection du plan (AEJ) et du plan (DCH) :
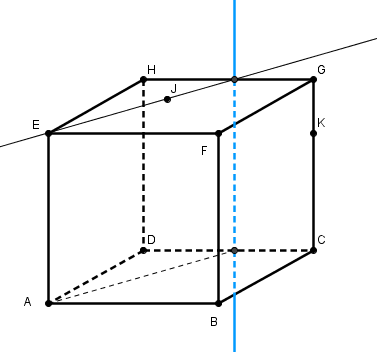
je te laisse poursuivre avec ce qui est demandé : intersection de (AJ) et (DCH)
vu que la droite (AJ) est dans le plan (AEJ) ça ne devrait pas être trop dur !
comprends tu au moins pourquoi (justifications) je prétends que ma droite bleue est l'intersection du plan (AEJ) et du plan (DCH) ?
parce que sinon ce n'est pas de l'aide dont tu vas avoir besoin
c'est carrément te faire l'exo avec une solution à laquelle tu ne comprendras rien.
ce qui ne t'apportera rien.
ensuite (AJ) fait partie du plan (AEJ) (!!)
la droite bleue fait partie du plan (AEJ), donc ces droites ...
dans quels plans (les citer tous) ce point ainsi construit appartient-il ?
etc.
oui Je comprends que la droite bleue est l'intersection du plan (AEJ) et du plan (DCH).
Je n'arrive pas à modifier ta figure . Comment on fait ?
tu n'arrives pas à quoi ??
l'exo se fait étape par étape
si tu cherches à faire tout d'un coup c'est impossible
donc "je n'y arrive pas" sans précision c'est renoncer à seulement chercher.
1ère étape je te l'ai donnée :
construire l'intersection du plan (AEJ) avec le plan (DCH)
1ère question : (réponds à cette question) justification de cette construction là.
pourquoi tel point est dans telle droite qui est dans tel plan
pourquoi des parallèles ?
pourquoi ces droites là se coupent "en vrai" (dans l'espace) (quel plan contient les deux droites)
à quoi ça va servir ?
l'objectif (dit dans l'énoncé) est de construire l'intersection de la droite (AJ) qui fait partie du plan (AEJ) avec le plan (DCH)
et on connait maintenant une droite (en bleu) qui fait à la fois partie de ces deux plans
ensuite on verra.
chaque chose en son temps
pour moi je ne vois pas d'intersection entre la droite (AJ) et le plan (DCH).
J'ai vraiment du mal à me progeter dans l'espace
OK, tu dis que tu as compris entre temps pour l'intersection de (AEJ) et (DCH).
la droite (AJ) est dans le plan (AEJ) (dans le nom du plan)
la droite bleue est dans le plan (AEJ) par construction (vu que c'est l'intesction de (AEJ) avec autre chose)
donc dans ce plan (AEJ) la droite (AJ) et la droite bleue se coupent ou sont parallèles. donc se coupent.
ce point appartient à (AJ)
il appartient à la droite bleue qui est aussi dans le plan (DCH)
donc ce point est l'intersection de (AJ) et du plan (DCH) puisqu'il appartint à la fois à (AJ) et à (DCH)
(et que (AJ) n'est pas entièrement dans (DCH) car A est en dehors)
tous les raisonnements sont de ce style là
choix d'un plan dans lequel on fait de la géométrie plane (les droites se coupent ou sont parallèles, dans un plan, Thales, parallélogrammes etc etc tout ce qu'on fait en géométrie plane)
inclusions de points dans des droites incluses dans des plans
intersections = appartient aux deux
quelques bons vieux théorèmes de géométrie dans l'espace concernant les plans parallèles et les plans orthogonaux
c'est tout.
Je n'arrive pas à modifier ta figure . Comment on fait ?
bein au plus simple tu l'ouvres dans Paint et tu ajoutes des traits (avec l'outil "trait", pas au crayon à main levée)
des pointillés sont obtenus en effaçant (gomme) des petits bouts du trait.
des points (en traçant des petits cercles avec l'outil cercle) et des noms (avec l'outil texte)
en cas de fausse manip rappel : la touche CTRL-Z annule la dernière opération.
la touche escape annule l'opération en cours.
sinon tu fais tout ça avec Geogebra en re-créant une figure du cube à partir de rien (ce que j'ai fait)
utiliser directement Geogebra 3D n'est pas la chose à faire car les plans sont entièrement "peints" par Géogebra et la figure devient vite "illisible"
même si Geogebra 3D trace directement les intersections sans même devoir réfléchir, de toute façon il faudra expliquer en ajoutant les traits de construction demandés.
par contre avec Geogebra 2D, il faut faire les pointillées soi-même (c'est un peu ch..)
Ok pour toutes ces infos.
Je pense pouvoir me pencher sur l'exercice plus sérieusement demain après midi.
Je reviendrais sûrement vers toi pour avoir d'autres infos
Merci encore
Ok pour toutes ces infos.
Je pense pouvoir me pencher sur l'exercice plus sérieusement demain après midi.
Je reviendrais sûrement vers toi pour avoir d'autres infos
Merci encore
Bonjour Mathafou
J ai essayé de continuer . Voici mon raisonnement :
Intersection du plan AEJ et DCH
Les points E et F appartiennent au plan AEJ et AEF.
Les deux plans AEJ et AEF ne sont pas confondus puisque le point J n'appartient pas au plan AEF.
Donc les plans AEJ et AEF sont sécant suivant la droite AE.
Comme ABCDEFGH est un parallélépipède rectangle les plans AEF et DCH sont parallèles.
Or si deux plans sont parallèles tout plan sécant à l'un est sécant à l'autre et les droites d'intersection sont parallèles.
Le plan AEJ coupe donc le plan DCH en une droite d parallèle à AE
Intersection de la droite AJ et du plan DCH dans le plan AEJ
La droite AJ appartient au plan AEJ .
La droite d appartient aussi au plan AEJ car c'est l'intersection de AEJ et DCH.
Donc le point d'intersection L des droites AJ et d appartient au plan AEJ et DCH.
Par conséquent l'intersection de la droite AJ et du plan DCH est le point L
Face DCGH
Je ne sais pas faire
Face FGCB
Le point K appartient au plan AJK et à la face FGCB.
Les plans BFG et AEH sont parallèles.
Or le plan AJK coupe le plan AEH en une droite AJ donc le plan AJK coupe le plan BFG en une droite parallèle à AJ . On obtient le point M. On peut tracer MK.
Face AEFB
Les points A et M appartiennent au plan AJK et à la face AEFB donc on peut relier AM
Face AEDH
En prolongeant la droite IK, IK coupe EH en un point N.
Donc les points A et N appartient au plan AJK et à la face AEDH.
On peut relier AN.
Il me manque la face DCGH
Est-ce que tu peux me dire si ce que j'ai fait est juste
il est impossible de faire les faces que tu as faites sans avoir au préalable la face DCGH
c'est bien pour ça qu'on commence par la demander dans l'exo
donc c'est faux
tu as tracé (LK) et ça ne t'a servi à rien ???
la droite (LK) est l'intersection de (AJK) et de (DCH) justement :
L est l'intersection de (AJ) qui est dans (AJK) avec (DCH)
donc ce point appartient à la fois à (AJK) et à (DCH) donc à leur intersection
comme K appartient de façon évidente à cett intersection
cette intersection est la droite (LK) (les plans ne sont pas confondus, et deux points déterminent une droite)
etc
pas le temps de détailler car je dois quitter jusqu'à demain
je pense avoir trouvé pour la face DCH :
Le point L appartient à la droite AJ et AJ appartient au plan AJK.
Soit O le point d'intersection de la droite HG et AL.
Le point O appartient à la face DCGH et au plan AJK car la droite AJ appartient au plan AJK.
Le point K appartient au plan AJK et a la face DCGH donc on peut tracer OK.
Quelques remarques à propos de la figure ci-dessus :
Tu n'as pas tracé l'intersection des plans (AEJ) et (DCH).
Les droites AN et KM devraient être parallèles.
L'intersection des plans (AJK) et(EFH) devrait passer par le point J.
Merci mathafou
J'ai corrigé certains points mais maintenant il me manque la face AEFB
Je te reposte mon raisonnement
Intersection du plan AEJ et DCH
Les points E et F appartiennent au plan AEJ et AEF.
Les deux plans AEJ et AEF ne sont pas confondus puisque le point J n'appartient pas au plan AEF.
Donc les plans AEJ et AEF sont sécant suivant la droite AE.
Comme ABCDEFGH est un parallélépipède rectangle les plans AEF et DCH sont parallèles.
Or si deux plans sont parallèles tout plan sécant à l'un est sécant à l'autre et les droites d'intersection sont parallèles.
Le plan AEJ coupe donc le plan DCH en une droite d parallèle à AE
Intersection de la droite AJ et du plan DCH dans le plan AEJ
La droite AJ appartient au plan AEJ .
La droite d appartient aussi au plan AEJ car c'est l'intersection de AEJ et DCH.
Donc le point d'intersection L des droites AJ et d appartient au plan AEJ et DCH.
Par conséquent l'intersection de la droite AJ et du plan DCH est le point L
Face DCGH
L est sur la droite d « 'intersection de (AJ) qui est dans (AJK) avec (DCH) »
Donc ce point appartient à la fois à (AJK) et à (DCH) .
K appartient au plan AJK et à la face DCGH
Par conséquent la droite (LK) est l'intersection de (AJK) et de (DCH) .
On peut donc tracer LK
Face FGCB
Le point K appartient au plan AJK et à la face FGCB.
Les plans BFG et AEH sont parallèles.
Or le plan AJK coupe le plan AEH en une droite AN donc le plan AJK coupe le plan BFG en une droite parallèle à AN . On obtient le point M. On peut tracer MK.
Face AEFB
?
Face AEDH
Les points A et N appartient au plan AJK et à la face AEDH.
On peut relier AN
Est-ce que tu peux m'aider .
Merci d'avance
LK : c'est juste.
Mais, ensuite, comment détermines-tu le point N ?
(note que je ne suis pas mathafou)
Je ne comprends pas.
A mon avis, tu ferais mieux, pour continuer après LK, de déterminer l'intersection des plans (AJK) et (FGC).
Tu pourrais tracer l'intersection des plans (AJK) et (FGC) si tu connaissais le point où le plan (AJK) coupe la droite (BF).
Pour cela, cherche l'intersection du plan (AJK) et du plan (ABF) en utilisant un théorème que tu as cité dans un message précédent.
Les plans ABF et DCH son //
LK est la droite d'intersection des plans AJK et DCH donc l'intersection des plan AJK et ABF est une droite // à LK
Je trouve que cette droite passe par le point B c'est bizarre non?
Oui, mais pourquoi par le point B ? C'est par le point A qu'elle passe, ce point appartenant aux deux plans.
Ok
Apres je fais l'intersection de cette droite avec BF et là problème
J'ai un point en dehors de la figure.
C'est ce point qu'il faut relier à K et qui sera mon point M?
Oui, la droite reliant ce point au point K coupe l'arête BC au point M, qui appartient à l'intersection du cube.
J'obtiens le même point M que celui que j'avais sur ma figure postée précédemment
Après je suis bloqué pour la face ABFE
L'intersection du cube ne passe pas par la face ABFE, hormis le point A.
Elle passe par contre dans la face ADHE.
En effet.
Pour construire le point N, il suffit de mener par le point A une parallèle à la droite KM; cette parallèle coupe l'arête EH en N.
Non. Après la face ADHE, l'intersection du cube continue sur la face EFGH.
Un point de l'intersection appartenant à cette face a été déterminé au début. C'est à ce point qu'il convient de relier le point N.
le problème est qu'on est parti sur de mauvaises bases au départ en voulant aller trop vite
la partie de section du cube par le plan (AJK) qui est située sur la face (DCH) n'a pas été déterminée
dans ces conditions tout devient énormément plus compliqué et sujet à erreurs.
on en est là (le reste à mon avis poubelle, mais je ne suis pas allé voir les détails)
on a construit l'intersection de (AEJ) avec DCH : la droite Δ
Δ est la parallèle à (AE) passant par I, intersection de (EJ) et de (GH)
puis l'intersection de (AJ) avec le plan (DCH) est le point L, intersection de (AJ) et de Δ (dans le plan (AEJ))
la droite (KL), située dans le plan (DCH) et le plan (AJK) est l'intersection de ces plans
elle coupe la droite (GH en un point que j'appelle P pour ne pas confondre avec d'autres
ce point est fondamental dans la construction
c'est à ça que servait la construction demandée dans l'énoncé
en effet la section du cube par le plan (AJK) sur la face [DCGH] est le segment [PK]
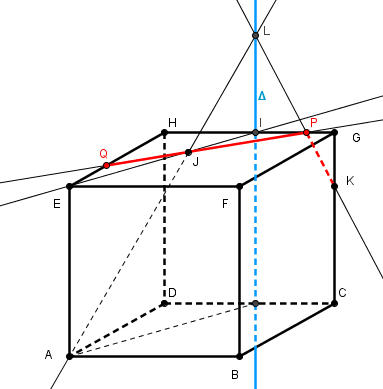
on peut alors terminer la construction "sans effort" !!!
en effet toutes les droites à tracer ensuite font exclusivement partie de la section cherchée
sont des droites passant par deux points connus de la section à la surface du cube
ou parallèle à une droite déja tracées par un point déja tracé de la section
par exemple la section du cube située sur la face [EFGH] contient le point J (il est bien sur cette face) et le point P (aussi)
donc c'est la droite (PJ)
elle coupe le bord de cette face en Q et la section sur la face [EFGH] est le segment [PQ]
etc...
on continue en cherchant la section sur [ADHE] : deux points connus lesquels ?
puis sur [BCGF] (un point connu une parallèle)
et on termine ainsi de proche en proche.
la section ne passe pas forcément par toutes les faces du cube
Section BCGF
BCGF est // à ADEH donc AJK coupe BCGF en une droite // à QA et passant par K et coupant BC
On obtient le point R
On trace KR
Pour la face ABEF je n'y arrive pas
Est-ce que ce que j'ai fait est juste et est ce que tu peux m'aider pour la face ABEF
OK
la section ne passe pas forcément par toutes les faces du cube
par contre il y a une face dans laquelle tu as désormais deux points connus ...
oui c'est bon (j'avais bien dit "OK", non ?)
c'est ton idée de vouloir absolument que la section passe sur la face (ABFE) qui est fausse
le plan (AJK) coupe le plan (ABFE) en une droite, que l'on peut tracer si ça nous chante,
mais qui ne comporte aucun point dans le rectangle ABFE.
et donc tracer cette droite ne sert à rien du tout.
d'où mon insistance à répéter que la section ne passe pas forcément par toutes les faces
par contre il y a une AUTRE face qui contient un morceau de la section
une face qui contient deux points déja connus et sur laquelle on n'a encore rien tracé, alors que juste joindre ces deux points terminerait complètement l'exo.
voila et c'est terminé :
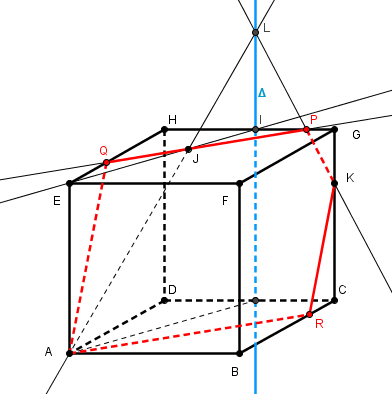
nota : AR est parallèle à PQ
l'exercice démarrait la construction par le plan auxiliaire (AEJ)
"Vous pourrez d'abord utiliser le plan (AEJ) pour tracer l'intersection de la droite (AJ) et du plan (DCH)"
ce n'est pas la seule méthode pour aboutir au résultat, mais comme c'était proposé dans l'énoncé, il fallait la suivre
et en tirer par contre les conséquences attendues sans dévier vers des itinéraires détournés : pourquoi donc l'exo nous demandait-il ce point si ce n'est pour l'utiliser ensuite de façon à simplifier le problème ?
on peut démarrer avec d'autres plans auxiliaires que (AEJ)
tu peux par exemple refaire l'exo en partant du plan auxiliaire GCJ pour obtenir l'intersection de (JK) avec le plan (ADH)
la suite sera du même genre mais on obtiendra notre section en commençant par le point Q au lieu de P.