Inscription / Connexion Nouveau Sujet
continuité convexité et fonctions
Propagation d'une maladie
Une epidemie a frappe les habitants d'une ville.
Le nombre de personnes malades en fonction du temps t, en jour, peut etre modelise par la fonction f, definie sur l'intervalle [0;30] par : f(x)= -t3+30t2.
La vitesse de propagation de la maladie au jour t est assimilee au nombre derive f'(t).
1) Etudier le sens de variation de la fonction f.
Ma reponse : f(x)=-t3 +30t2
f'(x)= -3t2+30*2t
= -3t2+60t
delta= (b)2-4ac
= (60)2-4*12*0
= 3600
delta>0
x1= b-Vdelta/2a= 60-V3600/2*3= 60-60/6=0
x2= b+Vdelta/2a= 60+V3600/2*3= 60+60/6= 20
tableau:
x 0 20 30
f'(x) + o -
f croissante decroissante
2) Determiner le nombre de solutions sur [0;30] de l'equation f(t)= 2000
determiner un encadrement a l'entier pres de la solution non entiere.
Reponse: je sais que les solution sont 10 et a peu pre 27 ou 28 car on le voit sur le graphique mais je ne sais pas comment faire.
3) a) Calculer la derivee seconde f"(t).
reponse: f(x)= -t3+30t2
f'(t)= -3t2+60t
f"(t)= -6t+60
b) Etudier le sens de variation de la derivee f'.
En deduire la convexite de la fonction f et en donner une interpretation.
Reponse: f"(t) >0 <=> -6t+60 >0
<=> -6t> -60
<=> t< 60/6
<=> t < 10
sur [0;10] la courbe est convexe entre le premier et le 10eme jour il y a une forte propagation de la maladie car la courbe croit.
c) Demontrer que la courbe C admet un point d'inflexion. En donner une signification concrete.
Reponse: f"(t)=0 <=> -6t+60=0
-6t=-60
t= 60/6
t= 10
La derivee seconde s'annule et change de signe en 10. Donc la courbe admet un point d'inflexion d'abscisse 10.
A partir du 10eme jour on a une croissance ralentie de la propagation de la maladie.
d)Calculer la vitesse de propagation de la maladie le 10eme jour.
Reponse: f'(t)= -3(10)2+60*10
= -3*100+600
= -300+600
=300
La vitesse de propagation de la maladie est de 300.
Merci de bien vouloir m'aider et de me signaler mes erreur pour pouvoir les corriger.
Salut,
1) Pour delta je suis d'accord (bien que ce soit )
Parcontre attention c'est -b+ .. et non b +
donc la reponse de x1 et x2 serait -20 et 0 mais ca va plus avec mon graphique aussi parce que j ai une courbe qui croit a partir de 0 et qui decroit apres a partir de 20
Faudrait que je le fasse avec les dérivées usuelles pour trouver les bon chiffres parce que je ne vois pas comment faire autrement que delta?
Merci d ´Avoir répondu et est e que mes autres question sont correctes ? Merci de bien vouloir répondre et de m indiquer ce qui éventuellement ne vas pas.
2) Determiner le nombre de solutions sur [0;30] de l'equation f(t)= 2000
determiner un encadrement a l'entier pres de la solution non entiere.
Reponse: je sais que les solution sont 10 et a peu pre 27 ou 28 car on le voit sur le graphique mais je ne sais pas comment faire.
La fonction f est strictement croissante sur ]0;20[ a valeur dans ]0;4000[ donc admet une solution sur cet intervalle pour f(x)=2000 (car
***Le site a détecté un multicompte***Situation à régulariser***cf Q29 de la FAQ : ![]() [lien]
[lien]
Bonjour j'ai un exercice un peu similaire, j'aimerai avoir une correction et j'ai une question sur une partie.
f(t)=-t^3+30t
1)nombre de malade au 6ème jour : f(6)= (-6)^2+30*6^2=1296 malades le 6ème jour.
2)dérivée f = -3t^2+60t
3) Déterminer une équation de la tenante de la courbe f au point d'abscisse 10. On la note F
F=300x-1000
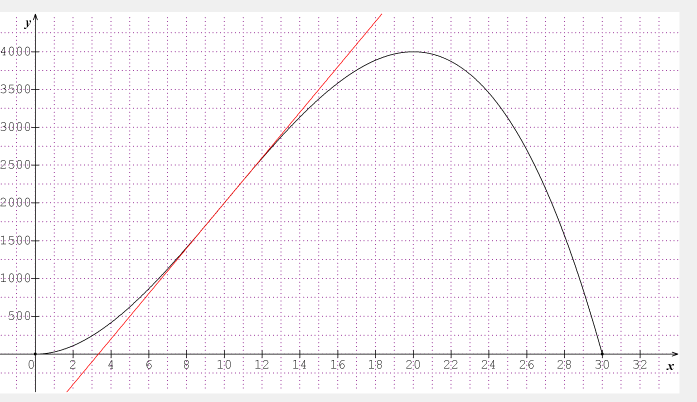
4) Sur la calculatrice tracer la courbe de la fonction et la droite F. Enoncer une conjecture sur la position relative de la courbe C par rapport à la droite F.
On l'impression que la tenante suit l'allure de la courbe.
5) Demontrer que f(t)-(300t-1000)=-(t-10)^3
J'ai trouvé : -t^3+30t-300t+1000=-t^3+30t^2-300t+1000
Donc les deux expressions sont égales mais je n'arrive pas à faire le lien avec ma conjecture. Merci
Bonjour j'ai le même exercice que la personne qui a posté le message précédent, j'ai compris le questions précédente mais je bloque sur la conjecture à faire. J'ai réussi à developper le calcul mais pareil je ne vois pas le lien. Merci par avance
Bonjour
Quel est votre profil exactement ? Vous postez en terminale et vous indiquez première.
Qu'avez-vous effectué ?
Bonjour j'ai un exercice un peu similaire, j'aimerai avoir une correction et j'ai une question sur une partie.
f(t)=-t^3+30t
1)nombre de malade au 6ème jour : f(6)= (-6)^2+30*6^2=1296 malades le 6ème jour.
2)dérivée f = -3t^2+60t
3) Déterminer une équation de la tenante de la courbe f au point d'abscisse 10. On la note F
F=300x-1000
4) Sur la calculatrice tracer la courbe de la fonction et la droite F. Enoncer une conjecture sur la position relative de la courbe C par rapport à la droite F.
On l'impression que la tenante suit l'allure de la courbe.
5) Demontrer que f(t)-(300t-1000)=-(t-10)^3
J'ai trouvé : -t^3+30t-300t+1000=-t^3+30t^2-300t+1000
Donc les deux expressions sont égales mais je n'arrive pas à faire le lien avec ma conjecture. Merci
Je vous prie de m'excuser pour le problème de compte, mais devenons-nous garder le même aussi quand nous allons sur la rubrique physique ?
Bonjour
Vous n'avez pas répondu à ma question : première ou terminale ?
Si vous êtes en première il eut été préférable d'ouvrir un autre sujet maintenant, c'est trop tard donc on continue ici.
Quel est le texte ?
Question 1
Question 2 oui si
Qu'est-ce qu'une tenante ? Je connais touchante ou tangente
C'est bien tentante excusez moi et je suis en première je ne savais pas qu'il fallait ouvrir un autre sujet.
f(t)=-t^3+30t^2, cette fonction modélise le nombre de malades en fonction du temps t
Question 1 f(6)=-6^3+30\times 6^2= 864
Question 2 donc la dérivée f = -3t^2+60t est d'ailleurs bien dérivable sur 0,30 inclus car elle est dérivable sur R
Question 3 Déterminer une équation de la tangente de la courbe f au point d'abscisse 10. On la note F
F=300x-1000
Question 4 : Combien de jours dure l'épidémie ?
Elle dure 30 jours
Question 5 : Sur la calculatrice tracer la courbe de la fonction et la droite F. Enoncer une conjecture sur la position relative de la courbe C par rapport à la droite F.
On l'impression que la tenante suit l'allure de la courbe.
Question 6 : Demontrer que f(t)-(300t-1000)=-(t-10)^3
J'ai trouvé : -t^3+30t-300t+1000=-t^3+30t^2-300t+1000
Non F est son nom ce n'est pas une équation de courbe équation de la tangente à la courbe au point d'abscisse 10
4) Quelle conjecture ?
C'est justement une interprétation de la tangente dans un petit voisinage autour de 10 on va pouvoir confondre la courbe et sa tangente
On peut dire que la tangente est la meilleure approximation affine de la fonction au voisinage de ce point
D'accord et ensuite on me demande de démontrer que f(t)-(300t-1000)=-(t-10)^3 et à partir de la je dois refuser ou valider la conjecture. Donc après développement les deux expressions sont bien égales et la conjecture est vérifiée.
Mais je pense que ce n'est pas suffisant pour répondre à la question non ?
On vous demande d'examiner la position de la courbe par rapport à sa tangente
On peut donc supposer que si la courbe est au-dessus de la tangente et pour
la courbe est en dessous de la tangente
Vous avez
le signe de ceci est le signe de donc
si Par conséquent l'ordonnée du point de la courbe est plus petit que l'ordonnée du point de la droite de même abscisse
La courbe est donc en dessous de la tangente
vous faites de même pour t>10
Si t>10 f(t) alors f(t)-(300t-1000)>0 donc l'ordonnée du point de la courbe est plus petit que l'ordonnée du point de la droite de même abscisse. La courbe est donc en dessus de la tangente
Non pour le message précédent
Si t>10 f(t) alors f(t)-(300t-1000)>0 donc l'ordonnée du point de la courbe est plus grand que l'ordonnée du point de la droite de même abscisse. La courbe est donc en dessus de la tangente
Oui, car j'ai oublié un signe c'était
c'est donc du signe de On retombe bien sur ce que l'on voulait montrer
J'avais aussi répondu sans regarder le dessin
le signe de ceci est le signe de 10-t donc
si t<10 f(t)-(300t-1000)>0 Par conséquent l'ordonnée du point de la courbe est plus grand que l'ordonnée du point de la droite de même abscisse
La courbe est donc en dessus de la tangente
Si t>10 f(t) alors f(t)-(300t-1000)<0 donc l'ordonnée du point de la courbe est plus petit que l'ordonnée du point de la droite de même abscisse. La courbe est donc en dessous de la tangente
Non aucun problème merci beaucoup pour votre aide.
La dernière question vise à modéliser la situation : Comparer la progression du nombre de nouveaux malades chaque jour avant le 10ème avec celle après le 10ème jour.
J'ai fait un tableau pour chaque jour avec les valeurs et j'ai dit que jusqu'au jour 10 le nb de malades augmente avec une moyenne de 200malades/j, au jour 10 c'est le maximum de malades. Puis jusqu'au jour 20, le nb diminue et enfin du jour 20 à 30, le nb de malades est négatif donc les gens guérissent. Est-ce une bonne manière de modéliser la situation ?
Jusqu'à 10 le nombre de malades croît, car dérivée positive ensuite le nombre de malades croît encore, la dérivée est toujours positive, mais plus lentement, après 20 le nombre de malades décroît, dérivée négative Ce n'est qu'après 30 qu'il n'y a plus de malades
Bonjour, j'ai moi aussi un exercice similaire est l'on me demande de démontrer pour tout t ∈ [0;30] : f(t)-(300t-1000)=-(t-10)²(t-10). En sachant que f(t)=-t³+30t². Merci d'avance pour votre aide
A droite de l'égalité vous avez donc développé ce qui donne des identités remarquables des deux côtés de l'égalité ? Je n'arrive pas à faire le lien...
Je n'ai rien développé. J'ai juste changé l'ordre des termes.
On peut remarquer que l'on peut mettre en facteur dans
Je vous ai donné l'identité pour que vous l'appliquiez à
.
Ensuite une autre factorisation
Cela donne donc 10^3-t^3=(10-t)(10^2+10t+t^2) ? mais grâce à cette identité je ne comprend pas comment je peut prouver l'égalité..
Je vient d'avoir une révélation ahah. J'ai trouvé la solution en fait au final j'ai trouvé la même expression après le développement de celles-ci. Merci pour votre aide précieuse ainsi que l'identité du cube que je ne connaissais pas du tout bonne soirée.