Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale ContinuitéTopics traitant de Continuité [tout]Lister tous les topics de mathématiques
Niveau terminale
continuité dans tout point de R
Posté par Khola22
Bonjour, j'ai un exercice devant moi qui me pose un problème :
Citation :
On considère la fonction h définie sur
par :
 = \frac{\sqrt{x}-1}{x^2-x})
si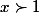 
= x^2+ax)
si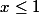 
1) Montrer que h est continue en tout point de ]-
;1[ et en tout point de ]1;+[
2) Determiner la valeur de a pour laquelle la fonction h est continue en tout point de.
On considère la fonction h définie sur
par :
1) Montrer que h est continue en tout point de ]-
;1[ et en tout point de ]1;+[
2) Determiner la valeur de a pour laquelle la fonction h est continue en tout point de
.
Bon je trouve que H est continue en tout point de R
a
R.
car si on reussit à démontrer 1), il restera seulement la continuité en 1,
et on a
et h(1) = 1+a.
Où est le problème ? Pourquoi a-t-on besoin de valeurs de a ?
Bonjour
Citation :
et on a = 1+ a)
et on a
Malheureusement, c'est faux. C'est seulement la limite à gauche.
Il faut aussi faire en sorte que la limite à droite soit la même pour que le raccord se fasse entre les deux morceaux de courbe...
Annuler
connectez vous