Inscription / Connexion Nouveau Sujet
Continuité de fonctions
Bonjour ,
Merci d'avance. 
Soit f la fonction définie sur par :
où a est un nombre réel.
Déterminer a pour que f soit continue en 1.
Réponses
f est continue en 1 <==>
* ,
.
* ,
Donc
Donc f est continue en 1 <==>
<==>
<==>
J'ai remplacé a par sa valeur et voilà ce que j'ai avec GeoGebra..
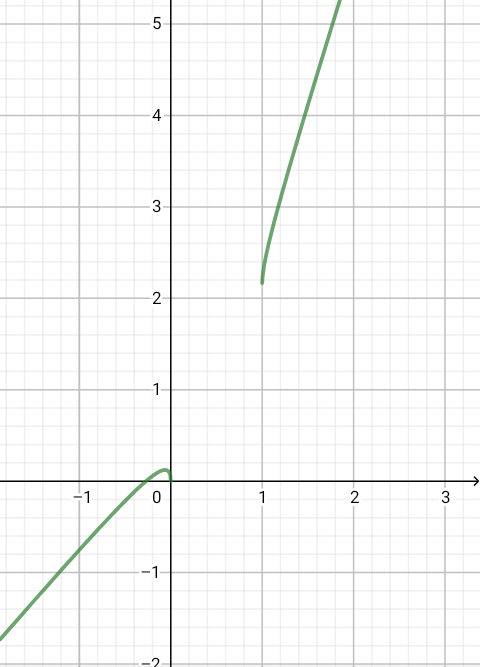
Il est clair que f n'est pas continue en a.
Ai je commis une faute dans mes calculs ?
Bonsoir, mais si ça marche, tu n'as pas dû rentrer les deux expressions correctement,
utilise f(x) = Fonction( Fonction , de , à )
on voit très bien la continuité en 1 avec le a que tu as trouvé.
salut
D'accord , et au niveau de la réaction ça va ?
on peut faire plus rapide :
posons
g est définie et dérivable sur R (à justifier)
et



