Inscription / Connexion Nouveau Sujet
Continuité et convexité
Bonjour, alors voilà, mon prof m'a donner un exercice pour m'entraîner pour un DS d'après rentrée et pour tout avouer a certaine question je suis complètement pommée :S Alors je vous préviens d'avance que mon exercice se compose en 3 parties et il est donc un peu long :C
Fabrication de tee-shirts
PARTIE A
Soit g la fonction définie sur [1;100] par :
g(x)=x3-1200x-100
1) Calculer g'(x)
J'ai trouver : g'(x)=3
1x²-1200
=3x²-1200
2)Étudier les variations de g et dresser son tableau de variation.
Alors pour cette question j'ai utiliser 
= b²-4ac
=3²-401200
=9-0
= 9
Ensuite pou x1 et x2 j'ai trouver x1= -1 et x2= 0 (je pense pas que ce soit juste et je n'arrive pas à savoir où je me suis trompée !!)
J'ai fait un tableau de variation : x -1 1 0 100
f'(x) - + -
f(x) \ / \
3)Montrer que l'équation g(x)=0 admet une unique solution 
dans l'intervalle [20;40]
Alors pour cette question j'ai fait l'équation mais je suis pas sûre de ma réponse :S
g(x)=0
g(x)=3x²-1200=0
-3x²=1200
x= 1200/-3
x= -400
4) Déterminer, à l'aide de la calculatrice, une valeur approchée de arrondie à l'unité.
cette question je ne sais pas comment faire
5) Déterminer le signe de g(x) sur [1;100].
Je pense que j'ai répondu avec mon tableau de la question 2 mais ça me parait bizarre !
PARTIE B
Soit f la fonction définie sur [1;100] par :
f(x)=x+50+1200x+50/x²
On note C sa courbe représentative dans un repère orthogonal d'unités graphique 1cm pour 5 unités en abscisses, et 1cm pour 20 unités en ordonnées.
1) Calculer f'(x) et monter que f'(x)= g(x)/x3
J'ai trouver un résultat bizarre :
U'V-UV'/V² = (1200)x²-1200X+50(2x)/(x²)²
= 1200x²-2400x²+100x/(x²)²
= -1200x²+100x/ (x²)²
2)Étudier le signe de f'(x) en utilisant les résultas de la question 5. de la partie A.
3)Dresser le tableau de variation de f sur [1;100]
Je pense que je saurais faire mais je suis pas sûre (en plus je crois que le resultat de la 1) est fausse :S)
5)Tracer la courbe C
6)Résoudre garphiquement l'équation f(x)=130 (on donnera des valeurs des solutions arrondies a l'unité) 
La je suis compltement pommé je sais pas comment faire !
PARTIE C
Une entreprise fabrique des tee-shirts; le coût total de fabrication de x centaines de tee-shirts est donné, pour x appartenant à [1;100] par C(x) = x²+50x+1200+50/x où C(x) est exprimée en euros. Le coût moyen de fabrication d'une centaine de tee-shirts, lorsque x centaines sont fabriquées, est défini par CM(x) = c(x)/x
1) déterminer la quantité de tee-shrits arrondie a l'unité à fabriquéer pour que le coût moyen soit minimal.
Là j'avouerai que j'ai m^me pas essayer parceque je ne sais pas comment m'y prendre :S
2) Préciser ce coût minimum pour une centaine de tee-shirts.
Voilà mon exercice, je sais qu'il est très long, et j'ai essayer de faire ce que je pouvais mais je le trouve quand m^me dur 
J'espère que vous pourrez m'aider, je ne demande pas les réponses juste qu'on m'aide à comprendre 
Merci d'avance 
Vous pouvez m'aider s'il vous plait ? Je sais que l'exercice est plutot long mais je l'ai pas super bien compris 
Bonjour Anais69
g'(x) est bien égal à 3x²-1200 que l'on peut écrire 3(x²-400)
3(x²-400) peut se factoriser à l'aide de la 3ème identité remarquable 3(x-20)(x+20)
ou alors avec le ( si on n'a pas reconnu l'identité remarquable )
On a a = 3
b = 0
c = -1200
Ainsi = 0²-4*3*(-1200) = 14400 = 120²
Merci beaucoup pour votre aide
alors j'ai refais et je trouve =14400
Pour x1 j'ai pour résultat -20
et pour x2=20
Je trouve mes résultats un peu bizarre étant donner que la fonction g est définie sur [1;100]
Mon tableau de variation donne ça :
x 20 1 20 100
g(x) - + -
g'(x) \ / \
Est-ce que c'est juste ?
J'ai fait partiellement le tableau de variations
Complète-le en plaçant aussi g(1) , g(20) et g(100)
3) Montrer que l'équation g(x)=0 admet une unique solution dans l'intervalle [20;40]
Calcule g(20) et g(40) , puis utilise le théorème des valeurs intermédiaires
Dans la ligne "Variations de g ", sous 1 , tu places g(1) , sous 20 , g(20) ( le minimum ) et sous 100 , g(100)
Ceci permet "d'encadrer" les valeurs prises par g(x)
g(20) et g(40) sont exacts
Donc , tu peux dire que comme 0 
[g(20) ; g(40)], on a [20;40]
Après , on utilise la table de la calculatrice pour cerner la valeur de
Ah d'accord
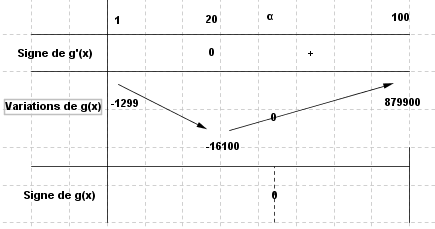
Donc g(1)=-199
g(20)=-16100
g(100)=879900
C'est ça ?
Alors pour la calculatrice je ne sais pas du tout comment m'en servir, notre prof ne nous as pas encore montré et quand j'essaye de taper dans table ça me met "syntax error"
Ah , c'est embêtant , je n'en ai pas sous la main , et de plus je connais assez mal les Casio 
En tout cas , la table indique que le passage en 0 se fait entre x = 34 et x = 35.
Voilà un extrait de valeurs obtenues avec un tableur
x g(x)
34,5 -436,375
34,6 -198,264
34,7 41,923
34,8 284,192
34,9 528,549
35 775
35,1 1023,551
Dans la question 4) , on demande d'arrondir à l'unité , donc on prendra = 35
Ensuite , on peut en observant les variations et les valeurs placées dans le tableau ,dire quel est le signe de g quand x < et quand x >
C'est négatif dans [1;35] , puis positif dans [35;100]
C'est en 35 que la fonction g change de signe
Ah d'accord oui car on change en et comme arrondi a l'unité est 35 alors on change la ok
j'ai compris merci
Cela vous dérange si vous m'aider a faire la suite ?
Il n'y a pas un petit oubli dans l'écriture de f(x)=x+50+1200x+50/x² ?( un carré qui se serait perdu ...)
Et quelle quantité se trouve sur le dénominateur x² ?
non pas d'oubli :S
f'(x)= x+50+ et après on a 1200x+50/x² Bien sur tout est attché mais je ne savais pas comment le mettre :S
Il y a 2 erreurs dans ce que tu as fait
Tu as oublié la dérivée de x+50 qui est 1
Puis , erreur de signe pour 100x ; c'est -100x
Donc f'(x) = 1 + (-1200x²-100x)/x4
= (x4 - 1200x² - 100x)/x4
= (x3 - 1200x -100)/x3
Hein oui c'est vrai :S
alors pour la question 2, on reprend le tableau du 5 et on calcul le signe ! J'ai trouver négatif dans [1;35] , puis positif dans [35;100]. C'est ça ?
C'est bien cela ! Donc on pourra en déduire facilement le signe de f'(x) , car x3 est positif dans le domaine d'étude
Donc , nouveau tableau de variation pour f cette fois , avec f' négatif de 1 à 35 , donc f décroissante , et f' positif de 35 à 100 et ainsi f croissante
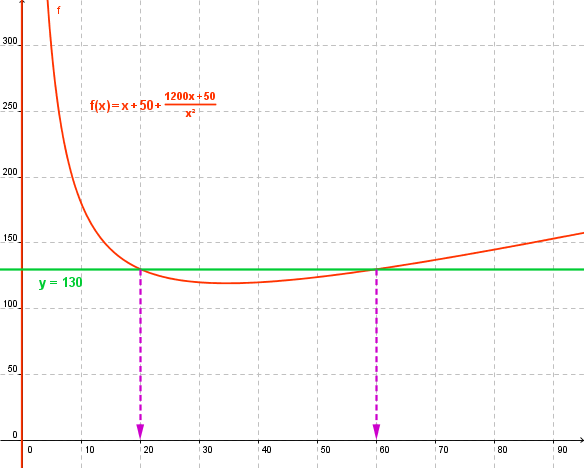
Pour la courbe et la résolution de la question 6 , je te joins la représentation graphique ( mais essaie d'apprendre à utiliser ta calculatrice !!! )
D'accord
Oui à la rentrée je demande a mon prof comment faire avec la calculette promis
Donc pour la 6) f(x)=130 avec pour solution 20 et 60 c'est ça ?
C'est ce qu'indique la lecture graphique .
Si tu calcules f(20) et f(60) , tu ne trouveras pas exactement 130
Ok comme on doit arrondir à l'unité Merci beaucoup
Vous pouvez juste m'expliquez les deux dernières questions ? si vous pouvez pas c'est pas grave
On a CM(x) = c(x)/x = f(x)
La fonction f(x) a déjà été étudiée , donc le coût moyen minimal est facile à trouver
Pour préciser la quantité de T-shirts à l'unité , on peut essayer de donner une valeur à 10-2 près de ( Ici = 35 correspond à 3500 T-shirts )
Autre extrait de tableur
34,64 -102,438656
34,65 -78,430375
34,66 -54,401304
34,67 -30,351437
34,68 -6,280768
34,69 17,810709
34,7 41,923
34,71 66,056111
34,72 90,210048
34,73 114,384817
Pour ce coût minimal , calcule CM(34,68)
Ça serait très cher pour un coût minimal de fabrication de 100 T-shirts 
Il faut encore diviser par 34,68 ( CM = c(x)/x )
Oui , c'est bon
Quand tu arrives au bout d'un calcul , essaie de voir si le nombre trouvé est possible ; ici , avec ce que tu proposais , le coût de fabrication d'un T - shirt aurait été de 41 € ; je n'ose imaginer le prix de vente ...
1) quantité de tee-shirts arrondie à l'unité : 3468
2) coût pour une centaine de tee-shirts : 119,32 €
OK merci beaucoup pour ton aide sans toi j'aurais été perdu maintenant j'ai tout compris! Tu explique bien mais sans donné les réponses c'est génial !
Encore merci ! 
)Bonjour j'ai eu le même sujet , merci pour les explications sans donner les réponse c'est génial !!
Mais pour ma partie C je dois donner le coup de fabrication de 500 tee shirt ( ma fonction est définie sur 1;1000
en faisant avec la formule c(x)= x²+50x+1200+50/x je trouve 276200.1 cela fait beaucoup je trouve
Annuler
connectez vous