Inscription / Connexion Nouveau Sujet
Continuité et Convexité
Bonjour, j'aurais besoins d'un peu d'aide pour me guider dans réalisation du devoir suivant:
Convexité d'une fonction
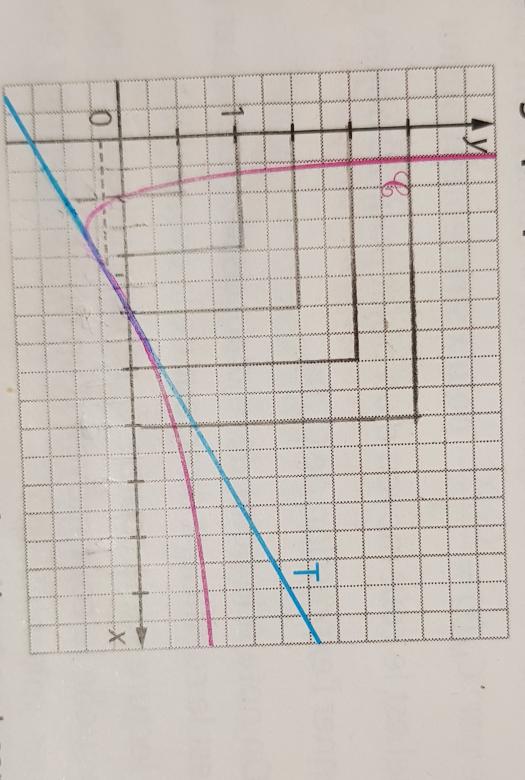
On considère la fonction g définie sur [; 10 ] dont la représentation graphique
(la courbe) C est donnée ci-dessous et T sa tangente au point d'abscisse .
On précise que g admet un minimum en et on donne:
g () = 5, g (
) = -
et g (10) =
Partie A. Étude graphique
1) À l'aide du graphique justifier que la fonction g est continue sur.
2) Lire graphiquement g'().
3) Dresser le tableau de variation de g.
4) En déduire le nombre de solutions de l'équation g(x) = 1.
5) Étudier graphiquement la convexité de g
Partie B. Étude théorique
On donne l'expression g (x) =
1) Montrer que g'(x) =
2)a. Montrer que g''(x) =
b. Étudier le signe de g''(x) sur [; 10 ] et en déduire la convexité de g.
c. Donner les coordonnées du point d'inflexion de (la courbe) C.
Travail réaliser jusqu'ici :
Partie A
1) On considéré la fonction g définie et continue sur [ ;10].
Pour tout réel k  [ g (
[ g () ; g (10) ]
l'équation g(x)= k admet au moins 1 solution dans [ ; 10].
D'autant plus que une fonction f est continue sur une intervalle si on peut dessiner son graphe sans lever le crayon d'un bout à l'autre l'intervalle ce qui est le cas de la fonction g.
2) L' antécédent de par g est
0,5
3) g - 
1,5 10 +

g(x) Décroissant Croissant
(Désolé je ne sais pas comment faire le tableaux de variations )
4) Une seule et unique solution est possible pour l'équation g (x) = 1
5) Soit une fonction g définie et dérivable sur un intervalle [ ; 10]. La fonction g est convexe sur [
; 1,5], car sa dérivé g' est croissante sur [1,5; 10] et représente un point d'inflexion en x = 1,5.
Partie B
1) On reconnait la fonction dérivable =
donc, nous avons : V(x) = U(x) =
+ 3
V'(x) = U'(x) = 4
g (x) =
g (x) =
Après cet exercice, c'est le néant je bloque à ce niveau d'ailleurs je ne sais pas si les réponses que j' ai mis avant ça sont juste.
Avant de continuer je voie que vous êtes passer directement à la première question de la partie b.
Es que cela signifie que les réponses que j'ai apporté aux questions de la partie À sont juste ?
d'ailleurs j'aurais besoin de savoir les réponses que j'ai donner pour la partie A sont juste s'il te plait
On donne l'expression g (x) =\frac{x^2-4x+3}{x^2}
On reconnait la fonction dérivable \frac{U}{V} = \frac{U' V - V' U }{V^2}
selon moi: V(x)= U(x)=
V'(x) = U'(x)=
V'(x) = U'(x)= 4
Mais, selon toi :
"On te donne g(x)=
" message de 09 : 06
D'où sort cette formule ?
et maintenant, tu développes le numérateur , tu simplifies
et
tu retrouveras
g'(x)=(2(2x-3))/x3
g"=...................à toi