Bonjour
Une indication : Dans le plan ABE on y=0 ......

J'ai trouver 3 points

S(0;0;3)
R(0;2;0)
P(1;0;0)
J'ai tracer .. les 3 points  et je n'arrive pas à tracer la section du cube en fonction de ce plan

Bonjour,
Tes points ne sont pas sur des arêtes du cube ; donc pas utilisables directement.
Il y a déjà le point B .
Ensuite on peut utiliser le point R : La droite (RB) coupe l'arête [CD] en J facile à préciser.
Idem avec la droite (BS) et une autre arête.

Ton point P est le sommet B

Du coup comment je fait pour la suite de la section ..?

Comme (RS) ne coupe pas le cube je fais comment ?

J'al fait :
•La parallele à (BK) sur le plan (JDC) qui donne un point I sur [GH]. Donc j'ai tracé [JI].

•la parallèle à (BJ) sur le plan (EFH) qui forme un point O sur [EH]. Donc j'ai tracé [KO]

• la parallele à (SR) qui fait [OI].

La section est un pentagone ?

Déjà, tu peux sur la figure tracer la parallèle à (BS) issue de J . En effet le plan D coupe deux plans parallèle en deux droites parallèles.
Idem avec K , le point obtenu sur l'arête [FE] : Tracer une parallèle à (BJ) .
Tu dois trouver ainsi le même point L sur l'arête [GH] .

Pour trouver ses coordonnées, deux méthodes :
Utiliser JBKL parallélogramme.
Trouver un système d'équation de la droite (GH) .

Je n'avais pas vu ton dernier message.
Je pense qu'on "tombe" sur [GH] les deux fois. Sur le point que j'ai noté L .
A vérifier.
Je ne vais plus être disponible pendant une petite heure ; mais tu m'as l'air bien partie

S'agit-il d'un quadrilatère (la section) ?

Oui, plus précisément un parallélogramme.

Bonjour,

Nota : si on considère les droites entières supports des arêtes du cube, les points initialement obtenus sont sur ces "arêtes" et donc permettent de tracer la section très facilement (à la règle seule).



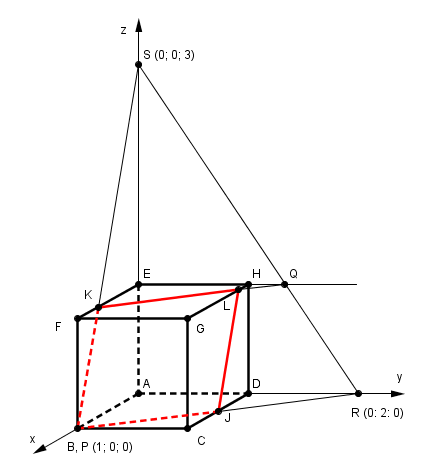
(noms en accord avec la discussion précédente sauf erreur, les mêmes points pouvant être obtenus de différentes façons)
l'idée dans cette construction ci est de ne pas avoir peur de "sortir" des faces du cube proprement dites mais de les considérer comme des plans infinis et les arêtes comme des droites infinies.

Jolie figure mathafou
S'appuyer sur le triangle PSR est effectivement un bon "plan" pour que tout s'éclaire.

Merci beaucoup à vous !