Inscription / Connexion Nouveau Sujet
Convexité et coûts totaux
Bonjour, j'ai un DM très important à rendre pour la rentrée et j'aurais besoin d'aide pour vérifié si mes résultats sont bien correct, ma moyenne en dépend, merci par avance !
Soit le sujet :
Un entreprise fabrique des objets et estime le coût total, en euros, de la production de x objets en fonction de x par : Ct(x) = x^3 - 60x^2 + 1500x + 5000 pour x[0 ; 70]
A. Etude de coût total
1. Déterminer le montant en euros des coûts fixes.
-> Les coûts indépendants de la production ; quand aucun objet n'est produit ; correspond donc à Ct(0) = 5000
2. Déterminer l'expression du coût marginal en fonction de x.
->Ici c'est la dérivée qu'il faut bien faire ? soit 3x^2-120x+1500
3. Déterminer les variations du coût total sur (0 ; 70)
-> Ici je ne suis pas sûr mais j'ai utilisé Delta où on a donc : b^2-4ac= 14 400 - 4x1500 = -3600
Donc la dérivée garde toujours le même signe et sachant que Ct(0)=5000 et que Ct(70)=159000 donc logiquement Ct'(x)>0 pour quelque soit x sur [0;70]
Donc le coût total est strictement croissant ?
4.a. Quelle semble être la convexité de Ct (la courbe est attachée au message en bas)
-> La courbe semble être concave puis convexe, on le prouve grâce à la dérivée soit :
Ct''(x)=6x-120
6x=120
x=20 donc 20 est le point d'inflexion
donc pour tout x appartenant à [0;20[ la courbe est concave et sur [20;70] la courbe est convexe ?
B. Etude du coût marginal
1. Calculer la dérivée de Cm en fonction de x
-> Il s'agît ici de reprendre Ct''(x) soit Cm'(x) = 6x-120 ?
2. Déterminer le sens de variation de Cm sur l'intervalle [0;70]
-> Est ce que ici on fait Delta à nouveau, delta de 6x-120 ?
Ca voudrait dire qu'on a 120^2 - 4( 6 * 0 )
soit Delta = 14 400 ?
Je ne sais pas si c'est bien ça qu'il faut faire et je bloque du coup sur cette question
3. Justifier l'existence d'un point d'inflexion de C et préciser l'abscisse de ce point
-> Du coup l'ayant déjà fait est ce que cela veut dire que je me suis trompé au paravent ?
Sinon je ramène juste les résultats trouver dans le 4)a) soit le point d'inflexion est pour x=20
4.a. A partir de quelle quantité produite, chaque objet supplémentaire produit est-il plus coûteux que l'objet précédent?
-> Il y a t-il un rapport avec les dérivées calculer auparavant / faut-il les mettre en commun ?
b. On appelle le rendement marginal le rendement prévu pour la production d'un objet supplémentaire.
-> Justifier l'affirmation suivante : "Pour une production de plus de 20 objets les rendements marginaux dans cette entreprise sont décroissants"
Est ce que il faut dire que la dérivée de Cm (6x-120) est positive à partir de x=20 donc les rendement marginaux dans cette entreprise sont décroissants ?
Il reste un petit C mais je n'y ai pas encore travaillé, j'attend d'abord de trouver entièrement le A & B, merci pour l'aide que vous pourrez m'apporter !
Bonjour,
A. Etude de coût total
Pour 1) et 2) c'est bon .
3) Tu as calculé le discriminant de la dérivée ; c'est juste .Comme celui-ci est négatif, on en conclut que cette dérivée est toujours du signe de "a", c'est à dire positive .
On a ainsi C't(x) > 0 pour tout x de l'intervalle , donc Ct(x) croissante .
et sachant que Ct(0)=5000 et que Ct(70)=159000 donc logiquement Ct'(x)>0 pour quelque soit x sur [0;70]
4) C'est juste
B. Etude du coût marginal
1) On a bien Cm(x) = 3x²-120x+1500 , donc C'm(x) = 6x -120
Pour 2) , on utilise donc cette dérivée 6x -120 pour déterminer les variations du coût marginal . Ici , pas de 
 . C'est une simple fonction affine dont il faut déterminer le signe .
. C'est une simple fonction affine dont il faut déterminer le signe .
Etudie le signe de 6x -120
Merci pour ta réponse !
Donc pour le 2) je fais un tableau de signe ? ce qui nous donnerais :
x -infini 20 +infini
Cm'(x) - 0 +
Attention , l'ensemble de définition se limite à [0;70]
Pour le signe , c'est juste .
Donc Cm décroissante de 0 à 20 , puis croissante de 20 à 70
3) Le point d'inflexion de C est bien en x = 20 ; il correspond à un Cm minimal ( et cette valeur x = 20 donne bien un Cm minimal si l'on regarde le tableau de variation )
D'accord j'avais un doute sur ça, merci !
Pour le 3) donc c'est juste ?
Et pour le 4)a) chaque objet supplémentaire produit est plus coûteux à partir de ce point d'inflexion ?
Oui , à partir de 20 objets , chaque objet supplémentaire est plus coûteux
Pour b) : on sait que les rendements marginaux sont décroissants lorsque le coût marginal est croissant ; or ceci est bien le cas pour une production de plus de 20 objets
D'accord merci pour le petit B !
Je me permet donc de mettre le C à la suite, qui me pose un peu plus de problème;
C. Etude du coût moyen
Le coût moyen d'un objet lorsque x objets sont produits est donné par CM(x)= Ct(x) / x pour x strictement positif.
1. Quel est le cout moyen d'un objet pour 20 produits?
Ici j'ai simplement remplacer x par 20 on a donc CM(20) = Ct(20) / 20 soit 19 000 / 20 = 950
2. Donner l'expression de Cm(x)
J'ai remplacé Ct(x) par sa vrai valeur ce qui nous donne : (x^3 - 60x^2 + 1500x + 5000) / x soit est égal à x^2-60x+1500+(5000/x)
3.a. On note A le point de C d'abscisse x. Expliquer pourquoi Cm(x)est le coefficient directeur de la droite (OA).
Alors là je ne suis pas trop sûr, mais je pense que :
La droite OA passe par l'origine du repère donc le coefficient directeur de la droite OA = yA/xA or, le point A d'abscisse appartient à la courbe C donc les coordonnées du point A sont A(x; C(x)) donc le coefficient directeur de la droite (OA) est égal à C(x) / x = Cm(x)
[]b.[/i] Par lecture sur la courbe C, semble-t-il exister une quantité x en laquelle le coût moyen d'un objet, lorsque x objets sont fabriqués, soit minimal ?
J'hésite ici, j'avais envie de dire que oui, il s'agît du point d'inflexion (x=20) mais si c'est ça, comment le justifier ?
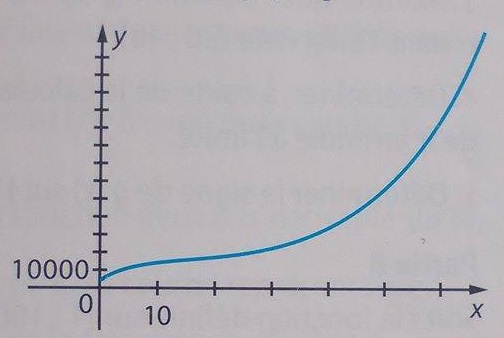
4. En utilisant la calculatrice et la courbe représentative de la fonction CM, déterminer un encadrement à l'unité près de la quantité à produire pour que le coût moyen de fabrication d'un objet soit minimal. (Vf la photo attachée)
A vrai dire je ne comprend pas vraiment cette question...
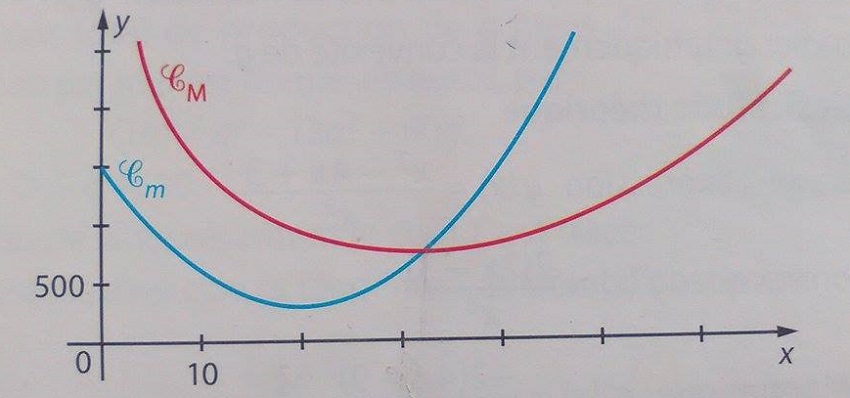
5. On a représenté Cm et CM dans le même repère
a. Tracer les deux courbes sur la calculatrice, puis déterminer une valeur approchée de l'abscisse alpha du point d'intersection entre ces deux courbes.
Je trouve approximativement alpha=32
b. Que représente alpha pour CM ?
C'est le coût moyen minimal pour un objet ?
6. On dit qu'une production se fait à rendement d'échelle croissants quand le coût moyen de production diminue, au fur et à mesure que la quantité produite augmente; chaque unité produite entraîne alors un coût moins cher que l'unité précédent.
Pour quelles productions d'objets peut-on dire alors que cette entreprise produit à rendement d'échelle croissants ? Justifier la réponse.
Je n'ai pas bien compris aussi cette question, est ce que c'est donc à partir du moment où le CM diminue c'est à dire jusqu'au point alpha = 32 ou après la courbe augmente ?
1) et 2) Très bien !
3)a) Oui , c'est juste ; on a bien une différence des ordonnées divisée par une différence des abscisses pour le coefficient directeur de la droite (OA), et donc ce dernier est égal à CM(x) ( attention à ne pas confondre le coût marginal Cm(x) ( dérivée de C(x) ) avec le coût moyen CM(x) qui est égal à C(x)/x )
b) Essaie d'utiliser le petit a) pour justifier ( ce n'est pas 20 ). Le coût moyen étant le coefficient directeur de (OA) , .......
Sur le graphique ci-dessous , j'ai tracé plusieurs segments [OA]
Observe les coefficients directeurs

Est ce qu'il s'agirait à nouveau de 32 ? car CM(32)=760.25 et CM(31)>CM(32)<CM(33) ?
Merci pour ton aide précieuse, je pense encore avoir besoin d'aide si cela ne te dérange pas bien sûr !
Bonsoir
A titre de contrôle :
Quantité *** Ct total *** Ct marginal *** Coût moyen
0 *** 5 000 *** ??? *** ???
1 *** 6 441 *** 6 441 *** 6 441,00
2 *** 7 768 *** 1 327 *** 3 884,00
3 *** 8 987 *** 1 219 *** 2 995,67
4 *** 10 104 *** 1 117 *** 2 526,00
5 *** 11 125 *** 1 021 *** 2 225,00
6 *** 12 056 *** 931 *** 2 009,33
7 *** 12 903 *** 847 *** 1 843,29
8 *** 13 672 *** 769 *** 1 709,00
9 *** 14 369 *** 697 *** 1 596,56
10 *** 15 000 *** 631 *** 1 500,00
11 *** 15 571 *** 571 *** 1 415,55
12 *** 16 088 *** 517 *** 1 340,67
13 *** 16 557 *** 469 *** 1 273,62
14 *** 16 984 *** 427 *** 1 213,14
15 *** 17 375 *** 391 *** 1 158,33
16 *** 17 736 *** 361 *** 1 108,50
17 *** 18 073 *** 337 *** 1 063,12
18 *** 18 392 *** 319 *** 1 021,78
19 *** 18 699 *** 307 *** 984,16
20 *** 19 000 *** 301 *** 950,00
21 *** 19 301 *** 301 *** 919,10
22 *** 19 608 *** 307 *** 891,27
23 *** 19 927 *** 319 *** 866,39
24 *** 20 264 *** 337 *** 844,33
25 *** 20 625 *** 361 *** 825,00
26 *** 21 016 *** 391 *** 808,31
27 *** 21 443 *** 427 *** 794,19
28 *** 21 912 *** 469 *** 782,57
29 *** 22 429 *** 517 *** 773,41
30 *** 23 000 *** 571 *** 766,67
31 *** 23 631 *** 631 *** 762,29
32 *** 24 328 *** 697 *** 760,25
33 *** 25 097 *** 769 *** 760,52
34 *** 25 944 *** 847 *** 763,06
35 *** 26 875 *** 931 *** 767,86
36 *** 27 896 *** 1 021 *** 774,89
37 *** 29 013 *** 1 117 *** 784,14
38 *** 30 232 *** 1 219 *** 795,58
39 *** 31 559 *** 1 327 *** 809,21
40 *** 33 000 *** 1 441 *** 825,00
41 *** 34 561 *** 1 561 *** 842,95
42 *** 36 248 *** 1 687 *** 863,05
43 *** 38 067 *** 1 819 *** 885,28
44 *** 40 024 *** 1 957 *** 909,64
45 *** 42 125 *** 2 101 *** 936,11
46 *** 44 376 *** 2 251 *** 964,70
47 *** 46 783 *** 2 407 *** 995,38
48 *** 49 352 *** 2 569 *** 1 028,17
49 *** 52 089 *** 2 737 *** 1 063,04
50 *** 55 000 *** 2 911 *** 1 100,00
51 *** 58 091 *** 3 091 *** 1 139,04
52 *** 61 368 *** 3 277 *** 1 180,15
53 *** 64 837 *** 3 469 *** 1 223,34
54 *** 68 504 *** 3 667 *** 1 268,59
55 *** 72 375 *** 3 871 *** 1 315,91
56 *** 76 456 *** 4 081 *** 1 365,29
57 *** 80 753 *** 4 297 *** 1 416,72
58 *** 85 272 *** 4 519 *** 1 470,21
59 *** 90 019 *** 4 747 *** 1 525,75
60 *** 95 000 *** 4 981 *** 1 583,33
61 *** 100 221 *** 5 221 *** 1 642,97
62 *** 105 688 *** 5 467 *** 1 704,65
63 *** 111 407 *** 5 719 *** 1 768,37
64 *** 117 384 *** 5 977 *** 1 834,13
65 *** 123 625 *** 6 241 *** 1 901,92
66 *** 130 136 *** 6 511 *** 1 971,76
67 *** 136 923 *** 6 787 *** 2 043,63
68 *** 143 992 *** 7 069 *** 2 117,53
69 *** 151 349 *** 7 357 *** 2 193,46
70 *** 159 000 *** 7 651 *** 2 271,43
Oui , pour la 3) b) , par lecture graphique , grâce aux coefficients directeurs , on peut estimer le coût moyen minimal se produisant pour x compris entre 30 et 35 objets
4. Il suffit de rentrer la fonction CM dans la calculatrice et utiliser la table .La courbe rouge présente bien un minimum aux alentours de x = 32
5.a) C'est correct
b) C'est le nombre d'objets à produire pour que le coût moyen pour un objet soit minimal .
Calcul de CM(32)
6.Une production se fait à rendement d'échelle croissants quand le coût moyen de production diminue
Sur quel intervalle , CM est-elle décroissante ?
CM est décroissante sur [0;32[ donc pour une production de 0 à 31 objets on peut dire que cette entreprise produit à rendements d'échelle croissants ? (pour justifier il faut dire que après l'intervalle [32;70] c'est strictement croissante ?)
Merci à toi macontribution :p
CM est décroissante sur [0;32[ donc pour une production de 0 à 31 objets on peut dire que cette entreprise produit à rendements d'échelle croissants ?
Oui , c'est juste
Bonne soirée !
Et un petit conseil : refais un exercice du même type ; c'est un grand classique