Inscription / Connexion Nouveau Sujet
Correction & Aide Exercice > .:Triangles Isométriques:.
Bonjour,
Durant les vacances j'ai des exercices sur les triangles isométriques à faire, et j'ai moyennement compris cette leçon. Je connais les théorèmes mais ce que je comprends moins c'est le plus dur, c'est à dire la rédaction.
L'énoncé de l'exercice :
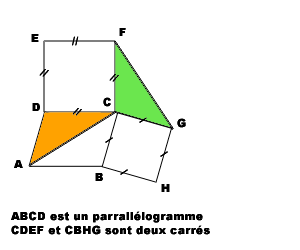
.: Voir Image attachée
1/ a) Démontrez que ^ADC^ = ^GCF^
..:: Info : Pensez aux angles supplémentaires en utilisant l'angle ^BCD^
b) Démontrez que les traingles ADC et FCG sont isométriques, déduisez en que ^ACD^ = ^CFG^ et que AC = FG
2/ La droite (AC) coupe (FG) en I
a) Démontrez que ^GFC^ + ^FCI^ = 90°
b)Déduisez en que les droites (AC) et (FG) sont perpendiculaires.
- - Ce que j'ai fais : - - - - - - - - - - - -
1/ a) Puisque ABCD est un parrallélogramme, ^ADC^ = ^BCF^
Donc, ^BCD^ + ^DCF^ + ^FCG^ + ^BCG^ = 360°
Et puisque ^DCF^ + ^BCG^ = 180°
Alors, ^BCD^ + ^FCG^ = 180° / 2 = 90°. Donc ^ADC^ = ^GCF^
J'ai rien compris à cette première question, et je crois que ce que j'ai fais est complètement faux car les angles ne sont pas plâts.
b) FC = DC
Puisque ABCD est un parrallélogramme : AD = BC = CG
Alors, AD = CG, FC = DC et ^ADC^ = ^FCG^
Les triangles ADC et FCG sont donc isométriques.
2/ a) Si ^GCF^ / 2 = 45° et que ^ACD^ = ^GCF^
Alors, ^GFC^ + ^FCI^ = 90°
b) Si ADC = ABC = FCG et que (AC) coupe (FG) en son milieu I.
Alors, (AC) et (FG) sont perpendiculaires.
Voila, si vous pourriez me corriger et si ce n'est trop demander, une petite aide mais je ne veux pas abuser 
Merci à vous.
Bonne soirée.
Bonjour
les angles DCG et ABH sont égaux puisque
(DC)//(AB) et (CG)//(BH)
si tu prends les angles en C et B qui avec ces 2 angles ont une somme de 360°, tu vois qu'ils sont composés de:
en C l'angle DCF droit et l'angle FCG
en B de l'angle HBC droit et de l'angle ABC
tu peux donc en déduire que
angle ABC=angle FCG
et comme dans le parallélogramme ABCD
angle ADC=angle ABC
on a bien
angle ADC=agle FCG
la suite est simple DC=CF (côtés d'un carré)
CB=CG (même raions) et comme
CB=AD (paralléogramme ABCD)
on a bien DA=CG
1 angle compris entre 2 côtés égaux
les triangles sont isométriques.
dans ta démonstration, je ne vois pas comment tu peux affirmer que
angle GCF=90/2=45° car ce n'est pas exact !!!
Pour revenir à la question posée
mène par D une parallèle à (AC) qui coupe (CF) en J et FG en K
et tu montres que les triangles DCJ et FJK ont les angles aigus égaux.
comme l'un est rectangle, l'autre le sera aussi
(angle en J opposés par le sommet et angle JDC=angle CAB=angle CFG)
la déduction est immédiate (AI) est perependiculaire à (FG)
c'est une règle générale.
deux angles dont les côtés sont perpendiculaires sont des angles égaux.
et réciproquement: si deux angles égaux ont deux côté perpendiculaires, alors les 2 autres le sont aussi
Bon travail
Merci de ton aide,
Vu comme ça, ça n'a pas l'air compliqué, mais sans un minimum de logique et de connaissances ce n'est pas évident à réussir à résoudre un tel exercice.
Petite question,
la suite est simple DC=CF (côtés d'un carré)
CB=CG (même raions) et comme
CB=AD (paralléogramme ABCD)
on a bien DA=CG
1 angle compris entre 2 côtés égaux
les triangles sont isométriques.
Le fait de dire que le triangle est isométrique ça prouve que ^ACD^ = ^CFG^ et que AC = FG ?
Enfin, oui ça le prouve mais faut-il justifier ?
Pour la quesiton 2 j'ai moyennement compris, mais je vais arreter pour ce soir et essayer de comprendre ça demain. Mais si j'ai bien compris il suffit de dire que :
DJ est parrallèle à AC et coupe (CF) en J et GF en K.
Et que, J est opposé au sommet D et ^JDC^ = ^CAB^ = ^CFG^
Et qu'on peut en déduire que (AI) est perpendiculaire à (FG) ?
Ca me parait un peu trop simple, enfin, je voudrais juste une confirmation. J'essairais de finir demain.
Merci à vous.



