Inscription / Connexion Nouveau Sujet
cosinus et sinus d'un nombre
bonjour mon professeur ma donné cet exercice et j'ai beaucoup de difficultés j'epère que vous pourrez m'aider 
!
enoncé :
dites si chacune des affirmations est vraie ou fausses. Justifiez
1) pour tout nombre x : (cos x)²+(sin x)²=1
2) il existe un nombre x tel que sin x = racine de5/2
3)Il existe un unique nombre x de l'intervalle [pi/2;3pi/2 ] tel que cos x =- 1/3
4) il existe un nombre x tel que sin x =cos x=0
Bonjour,
Je ne sais trop quelle est la meilleure façon de t'aider ... les questions sont assez proches de ce qui doit être le contenu du cours.
Alors on va essayer autre chose 
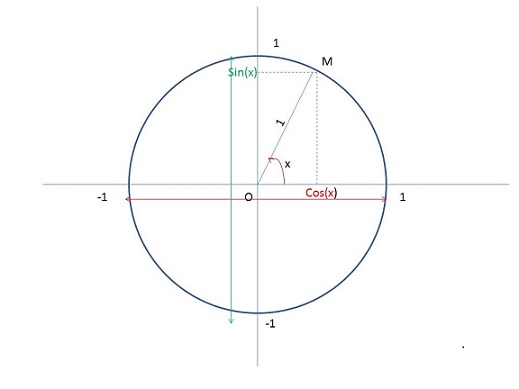
1) tu dessines un cerce de centre O et de rayon 1
2) tu fais circuler sur ce cercle un point M.
Ton nombre x c'est l'angle que fait OM avec l'axe des abscisses.
Alors le cosinus(x) c'est l'abscisse de M, sinus(x) c'est l'ordonnée
Comme ton rayon a pour longeur 1: cos2 + sin[sub]2[/sup] = ...
Pour la même raison est ce que le sinus peut ête plus grand que 1 ou plus petit que -1?
si le sinus vaut 0, que vaut le cosinus?
...
Est ce plus clair?
Bonjour etant donné que je n'ai pas eu de cours je ne comprends pas les formules que vous donner tout est assez confus 
Bonjour
Aïe ...
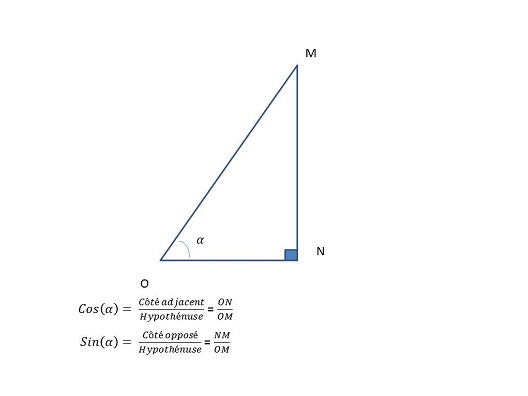
Te souviens tu de ton cours de 3ème? Le prmier dessin ci dessous pour le résumer: il te définit le cosinus et le sinus dans le cas d'un triangle rectangle.
Je considère que cela est OK (si ce n'est pas le cas, il faudra creuser pour trouver un autre moyen de te faire avancer dans la résolution de ton exercice)
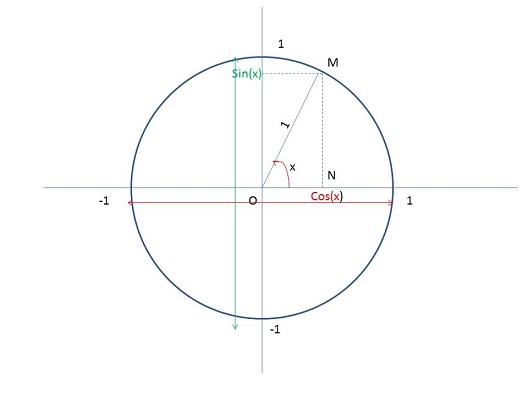
Tu remarques alors que dans la figure précédente, que j'ai reproduit également ci dessous -2eme dessin-, j'ai ajouté sur l'axe des abscisses le point N
Si tu applique les règles de trigonométries que nous venons de revoir et comme OM = 1
le point M a pour coordonnnées, dans le repère dont nous avons donné les axes dans la figure, M(cosx,sinx)
Partant de là
ONM est un triangle rectangle en N et Pythagore te dit "somme des carrés côtés adjacents à l'angle droit = carré de l'hypothénuse"
ON2 + NM2 = OM2
donc cosx2 + sinx2 = 1. On vient de répondre à la suestion 1)
2) quand x varie (sur la figure x correspond à un angle) le point M va "tourner" le long du cercle qui a pour rayon ... 1!
donc cosx et sinx, varieront entre -1 et 1. On ne peut avoir cosx > 1!!!
Je passe les question 3) et 4) pour le moment nous y reviendrons plus tard (lorsque tu auras confirmé que tu as mieux compris)
Alors? c'est plus clair?
Super!
Attaquons alors 3 et 4:
Tout d'abord, tu as maintenant compris que nous avons représenté le réel x par un angle...
Un tour complet correspond à la valeur 2 x 
6,28
50 tours correspondront à x = 100, ...
Inversement le nombre x = 256 correspondra à 40 tours + qlq chose (80 + 4,6725...)
Donc le nombre 256 et le nombre 4,6725... auront même sinus et cosinus
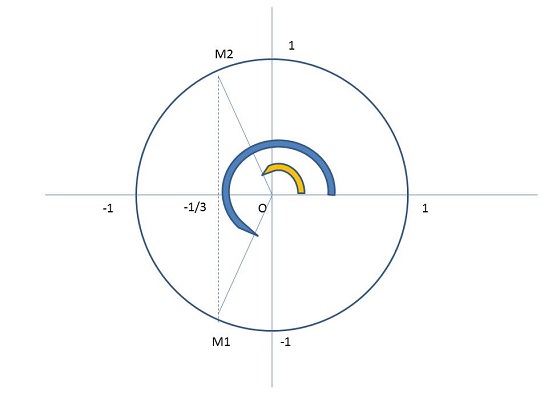
Tout cela pour expliquer que l'équation cos x = -1/3 aura une infifinté de solutions, mais qu'à l'intérieur d'un intervalle de longeur 2 (un tour donc), nous n'en trouverons que ... deux!
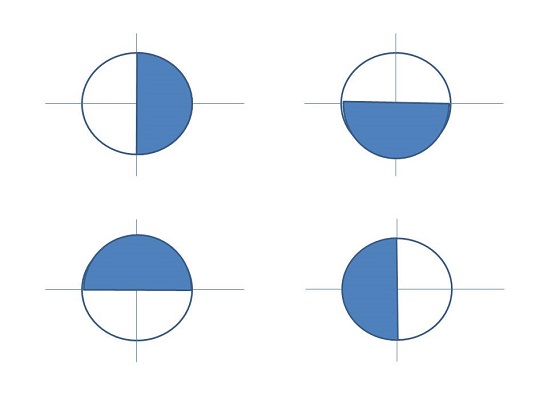
A l'intérieur d'un intervalle de longueur , les possibilités sont multiples ... puisqu'il existe 4 facons de positionner un intervalle de longeur (cf. second schéma ci dessous). Tu as donc en théorie 0 ou bien 1 ou bien 2 racines.
Dans la question qui t'est posée, l'éaqution cosx = -1/3 sur l'intervall[/2;3/2] il y a deux racines, une pour laquelle sinx > 0 et l'autre pour laquelle sinx < 0
Tu auras alors sans soute compris que cosx = sinx = 0 est impossible!
Annuler
connectez vous