x(t) est périodique de période (2pi/3)

y(t) est périodique de période (pi)

donc la fonction est périodique de période le ppcm des deux périodes précédentes (abus de langage car ce ne sont pas des entiers), c'est-à-dire ici 2pi effectivement

je n'est rien compris .

pourquoi 2pi/3 .
fin je ne voulais pas qu'on me donne le résultat sans explication .
je préfère même que tu ne me donne pas le résultat et que à la place tu m'aide .

Il m'avait pourtant semblé t'aider... désolé de t'avoir fait perdre ton temps, salut !

tu me donneme donne simplement la réponse alors que je ne comprend pas comment déterminer l'intervalle d'étude .

oua la réaction de gamin .

quelqu'un pourrait m'expliquer comme a fait blumaise ?

salut

la définition d'une fonction périodique permet de comprendre la réponse de blumaise ...

et tu es en math spé .... pour faire quelque chose qui se faisait au lycée ... il fut un temps ...

ce que j'ai pue comprend seul c'est que :

quand t parcoure [-/3;/3]

alors 3t parcoure [-;] donc cos(3t) parcoure une période . donc tout les 2/3 cos(3t) se répète .

pour sin(2t) c'est tout les qu'il se répète .

donc on recherche un intervalle dans lequel x et y finissent en même temps leur période . donc on prend 2 . pour ma dernière phrase je ne suis pas sûr .

Bonjour.
Blumaise t'a donné les périodes de x(t) et  y(t). La fonction f(t)=(x(t),y(t)) ne sera périodique que si les  2 périodes sont commensurables d'où son "ppcm".

BOnjour

pour répondre à ta première question :

une fois la période déterminée : on la répartit de manière symétrique autour de 0, hiqtoire de pouvoit utiliser les parités éventuelles de x et de y

ici, on va donc commencer par regarder l'intervalle [-pi;pi], qui par périodicité donnera toute la courbe

ensuite, on regarde si x et y sont paires ou impaires

ici, quand on change t en -t, x ne change pas, y est changé en son opposé : il suffira donc de faire l'étude sur [0;pi], et on aura l'arc de courbe correspondant à l'intervalle [-pi;0] grâce à une symétrie par rapport à l'axe (Ox)

ensuite, pour tenter de réduire encore, on va chercher à voir ce qui se passe si on remplace t par pi - t (si t va de 0 à pi/2, pi - t va aller de pi à pi/2)

ici, cos(3(pi-t)) = cos(3pi - 3t) = cos(pi - 3t) = -cos(3t) donc x est changé en son opposé
et sin(2(pi-t)) = sin(2pi - 2t) = sin(-2t) = -sin 2t : y aussi est changé en son opposé

il suffit donc de faire l'étude sur [0; pi/2], puis on obtiendra l'arc correspondant à [pi/2; pi] grâce à une symétrie centrale de centre O.

si on veut, on peut encore chercher à réduire en regardant ce que donne le changement t en pi/2 -t

cos(3(pi/2-t)) = cos(3pi/2 - 3t) = cos(-3t-pi/2) = cos(3t + pi/2) = -sin(3t) : ça ne donne rien, ça ne ressemble ni à +/-x ni à +/-y

donc étude sur [0; pi/2] puis symétrie centrale de centre O puis symétrie axiale d'axe (Ox) pour obtenir toute la courbe.

salut . merci beaucoup lafol .

moi quand je faisais x(pi-t) et y(pi-t) et bein je disais juste que l'intervalle était diviser encore par 2 mais je n'y réfléchissais pas et donc j'ai defois je le divisais pas 2 et c'est faux .

dans notre cas , on est après symétrie par Ox sur [0;pi]
puis on a : x(pi-t)=-x(t) et y(pi-t)=-y(t) .
donc symétrie par rapport à la droite -x .
mais juste comment vois tu qu'on peut passer de [0,pi] à [0,pi/2] ?
parce que moi qui suis un élève j'ai pas les réflexe que tu as et donc il faut que je le comprenne bien pour pouvoir le ressortir .

fait un petit dessin à chaque fois, pour voir où sont les points M(x(t),y(t)) et M'(x(t'),y(t')) l'un par rapport à l'autre :

avec t' = -t, M(x,y) et M'(x;-y) : ils sont symétriques l'un de l'autre par rapport à l'axe horizontal
donc quand t décrit [0, pi], t' décrit [-pi, 0], et M' décrit l'arc symétrique par rapport à l'axe horizontal de l'arc décrit par M

avec t' = pi - t, M(x,y) et M'(-x,-y) : ils sont symétriques par rapport à l'origine du repère
donc quand t décrit [0, pi/2], t' décrit [pi/2, pi], et M' décrit l'arc symétrique par rapport à l'origine de l'arc décrit par M

remarque bien que je n'ai pas parlé de symétrie par rapport "à la droite -x" (je me demande bien ce que peut être la droite -x, soit dit en passant)

pour la t'=-t je comprend qu'il suffit juste de prend la partie positive . sa me semble évident . car un fois tracer sur + et bien pour avoir la courbe sur - il suffit de faire une symétrie .

mais par contre pour t'=pi-t ou t'=(pi/2)-t c'est beaucoup moins évident . car pi-t par rapport à t c'est compliqué de voir ce que c'est .

j'ai vais essayer de comprendre avec des schéma comme tu me le propose .

dis toi bien que t ne se voit pas sur la courbe ! on ne voit que x et y
je ne sais pas si le jeu "télécran" existe toujours ? une courbe paramétrée, c'est un télécran : x(t) dit à quelle allure tourner la molette du déplacement horizontal, et y(t) dit à quelle allure tourner celle du déplacement vertical
quand tu as fini le dessin, tu n'as plus aucune indication de dans quel ordre tu l'as fait, tu ne vois plus quie les points (x,y), plus trace de t

donc dans les petites dessins que je te dis, M(x,y) et M(x,-y) sont symétriques l'un de l'autre par rapportà l'axe horizontal : de l'instant -pi à l'instant 0, tu as tracé un dessin sur ton télécran, et de l'instant 0 à l'instant pi, tu traces avec ton télécran le symétrique de ce dessin par rapport à l'axe horizontal

M(x,y) et M(-x,-y), eux, sont symétriques par rapport à l'origine : ça veut dire que de l'instant 0 à l'instant pi/2, tu as fait un petit dessin, et de l'instant pi/2 à l'instant pi, tu as fait le symétrique de ce dessin par rapport à l'origine

on peut aussi dessiner la courbe sur geogebra ou sine qua none pour voir les éventuelles symétries

et en créant un point libre sur la courbe et en l'animant on peut voir encore plus mieux bien ces  propriétés

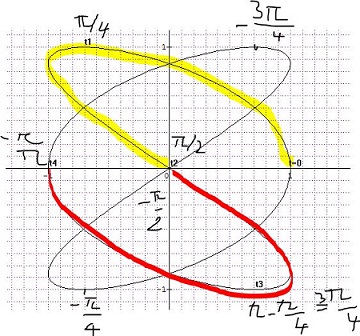
en jaune : de 0 à pi/2
en rouge : de pi/2 à pi
en noir : de -pi à 0

les temps de passage gribouillés à côté des points

je ne connais pas ce jeu .

en faite quand on a . [0,pi] que l'on a une symétrie en faisant t'=pi-t et bie il faut trouver un intervalle sur [0,pi] tel que  0<=pi-t<=pi .

c'est si compliqué que ça de voir que si on pose f(t) = pi - t, l'image de [0, pi/2] par f sera [pi/2, pi] ?

de manière générale, si tu en es à "étude sur [0;a]", pour voir si tu peux réduire encore, tu as le choix entre poser t' = t + (a/2), ou t' = a-t : si un de ces changements donne quelque chose, tu peux faire ton étude sur [0; a/2] puis effectuer la symétrie observée
avec les fonctions trigo, statistiquement, le changement t' = a-t donne plus souvent de bons résultats ....

une fois qu'on a l'intervalle on comprend mais quand on doit le trouver c'est différent . Surtout quand on commence juste à manipuler cela .

merci pour ton aide .

ça va venir, t'inquiète pas trop, et pense à faire des dessins pour voir quelle symétrie tu obtiens en faisant tes changements t - > t'