Inscription / Connexion Nouveau Sujet
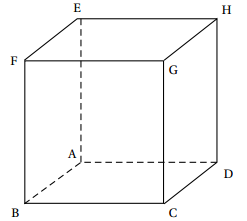
cube
Bonjour, j'aurais besoin d'aide pour cet exercice s'il vous plait :
Soit ABCDEFGH un cube. On définit les points M et N par 
MF =
1/4GF, et BN = 1/4BA.
1. Montrer que MN = F B + 1/4 GE.
2. En déduire que les vecteurs F B, MN, et GE sont coplanaires.
3. On note I le milieu du segment [BC]:
a. Démontrer que les droites (MI) et (BF) sont sécantes en un point L.
b. Montrer que les vecteurs BL et BF sont colinéaires et déterminer le réel k tel que BK=kBF.
c. Construire, sur la figure et en laissant apparents les traits de construction :
- le point L
- l'intersection D des plans (IMN) et (ABF) : expliquer comment est obtenue cette intersection.
- la section du cube par le plan (IMN).
il faut prendre des initiatives !
tu veux MN en fonction de FB et GE donc il va falloir décomposer MN avec Chasles
MN = MF + FB + BN = GF/4 + FB + BA/4 = FB + (GF+BA)/4 = FB +(GF+GH)/4 = FB + GE/4
(en vecteurs)
essaye de continuer, c'est plus simple après.
bonjour, merci pour vos messages j'avais oublier de préciser que j'avais déjà fait la question 1 et 2.
la question 3 me pose problème
je voulais prendre le repère (A; AD;AB;AE) et ensuite prendre les coordonnées de chaque point c'est ça ?
MI et BF sont toutes les deux dans le plan BCGF donc si elles ne sont pas parallèles, elles se coupent forcement.
BL et BF sont colinéaires puisque les 3 points sont sur une même droite.
après tu parles de BK = k BF tu as dû vouloir écrire BL = k BF ?
non tu n'as pas besoin de coordonnées, tu dois pouvoir trouver k juste en décomposant les vecteurs
(et peut-être en calculant LF avec Thalès par exemple : LF/LB = FM/BI = (1/4)/(1/2) =1/2
donc en fait LF = FB)
oui mais le point L on ne l'a pas encore c'est le point d'intersection des droites (MI) et (BF)
je comprend rien
et non c'est bien BK= kBF
*******
et non c'est bien
BK= kBFsurtout qu'il n'y a pas de point K dans cet exercice !! voyons!.....
Annuler
connectez vous