Inscription / Connexion Nouveau Sujet
cube _ plan sécant
Bonsoir, j'aurais besoin d'aide sur cette exercice :
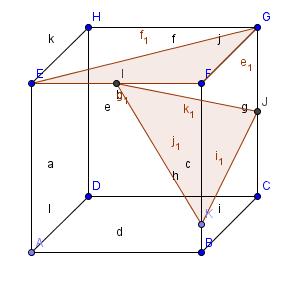
ABCDEFGH est un cube, I milieu de [EF] et J milieu de [CG]. K est un point de [BF] tel que BK = 1\6 de BF.
1) Démontrer que les plans (IJK) et (EFG) sont sécants puis déterminer leur intersection. Construire cette intersection que l'on nommera Alpha.
2) Démontrer que les plans (IJK) et (ABC) sont sécants puis déterminés leur intersection. Construire cette intersection que l'on nommera Alpha'.
3) Que peut-on dire de: Alpha et Alpha'? Le démontrer.
Merci d'avance si vous pouviez m'aider
Bonsoir ,
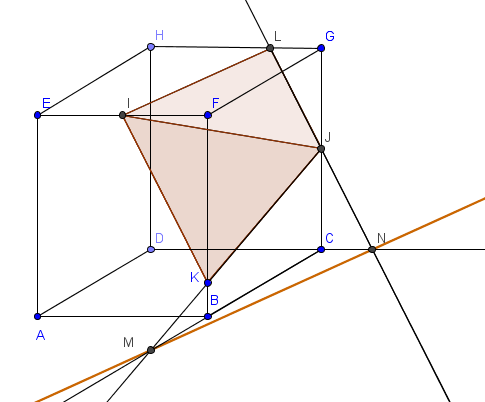
1) Les plans (IJK) et (EFG) ont le point I en commun . De plus , on sait que si un plan est sécant à 2 plans parallèles , les droites d'intersection seront parallèles . Ainsi , on peut définir le point L , avec (LJ) parallèle à (IK)
(IL) est l'intersection de (IJK) et (EFG)
2) pour trouver l'intersection entre (IJK) et (ABC) , on peut prolonger (JK) et (CB) , et définir leur intersection M ; de même avec (LJ) et (DC) pour obtenir N
La droite (MN) est l'intersection de (IJK) et (ABC)
Deux plans sont sécants s'ils ne sont pas parallèles .
Ici , on avait le point I en commun , donc pas de parallélisme au sens strict ( on pourrait avoir (IJK) = (EFG)); de plus J 
(EFG) , donc les plans ne sont pas non plus confondus .-----> (IJK) et (EFG) sécants
Le plan (IJK) coupe les 2 plans (ABFE) et (DCGH) ( qui sont parallèles car on est dans un cube ) selon des droites parallèles ( voir la propriété citée hier )
Donc il suffit de faire passer par J la parallèle à (IK) pour déterminer L
N'hésite pas à redemander si tu n'as pas compris
Merci grâce à vous j'ai enfin fini les questions 1) et 2). pouviez-vous m'aider pour la question 3) merci d'avance
Les plans (EFG) et (ABC) sont parallèles
(IJK) coupe ces 2 plans en 
et '
On utilise encore ici la propriété indiquée le 29-10-13 à 21:09
Donc les 2 droites sont .....
Annuler
connectez vous