Bonjour à vous,aucunes suggestions?

Cordialement,

Bonsoir,

malgré la mauvaise définition des images, des suggestions sont possibles bien que le travail à effectuer ne soit pas bien défini.
S'il s'agit de positionner les cercles (C₀) à (C₉) qui délimitent les 9 tronçons, positionner d'abord les points de contacts avec la pièce 3 (virole de diffusion) en traçant une ligne hélicoïdale de pas 4*338/3 sur un cylindre de diamètre 500
Ceci permet de déterminer la ligne entre chaque centre de cercle et son point de contact. La tangente à la ligne hélicoïdale au point de contact fixe le plan de chaque cercle. Le diamètre de chaque cercle est donné.

Mais quel genre de surface doit joindre les cercles extrémités de chaque tronçon ? surface développable ?
avec une ligne qui joint les points de contacts et qui ne peut être une droite ?

Bonsoir Vham,tu veux dire que chaque plans des cercles de bases des tronçons sont perpendiculaire à la ligne hélicoïdale?Concernant ta questions,je ne sais pas,mais il est demandé au candidat de Tracés des intersections et développés des surfaces.

re Bonsoir,

Ce n'est pas vrai pour (C₀) et (C₉) dont les plans sont imposés, pour les 8 autres cercles on peut sans doute choisir une rotation régulière autour de la ligne contact-centre par rapport au cercle précédent.

Bonsoir Vham,comment déterminer les Vraies grandeurs des contours de chaques tronçons?

Cordialement

Bonjour,

J'ai mieux relu le premier post car je n'avais pas fait attention au niveau BTS.
Ne s'agit-il pas de reprendre tout simplement en géométrie descriptive les 2 vues cotées dans l'encadré :
     Définition du cyclone hélicoïdal, repère 1

Essai en utilisant GeoGebra : J'ai  considéré que les 10 cercles des tronçons ont des diamètres qui vont de 450 à 180, sont centrés vus de profil sur un cylindre d'axe définis par O1 et de diamètre 750. Alors ces cercles ne sont pas tangents au cylindre d'axe 02, de rayon 500, comme le laisse supposer la vue en bas à gauche

Quels sont les outils de dessin dont vous disposez ? table à dessin, logiciel ? A vous donc.

Bonsoir Vham et merci.Oui,effectivement, on pourrait reprendre cet exercice en géométrie  descriptive  pas à pas.Sinon je travaille sur un logiciel CAO /DAO  spécialement conçu par des tôlier pour des tôlier.

Cordialement,

Bonjour,

le problème est déja que ce ne sont pas des cercles mais des ellipses ...

Bonjour Mathafou,Ah bon?les bases des tronçons seraient elliptiques?Comment le détermines-tu?C'est peut être à cause des plans de coupe?

Bonne journée !

Cordialement ?

si les plans de coupe ne sont pas perpendiculaires à l'axe des troncs de cône la section est une ellipse, propriété bien connue et "par définition" des sections de cônes par un plan, alias coniques.
(on ne va pas jusqu'à l'incliner tant que ça devienne des paraboles et hyperboles !)

tracer la forme de la section sur le patron (développé) ne se fera que point par point.
par exemple en reportant sur l'épure la construction suivante de l'espace :



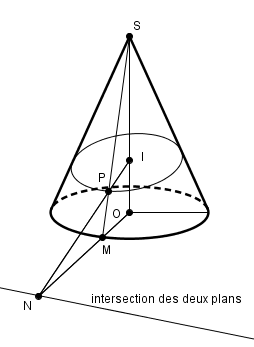
ou peut être une construction basée sur les sphères de Dandelin. (tangente au cône et au plan de coupe) dont les points de contact avec le plan sont les foyers de l'ellipse

cordialement

Bonjour,

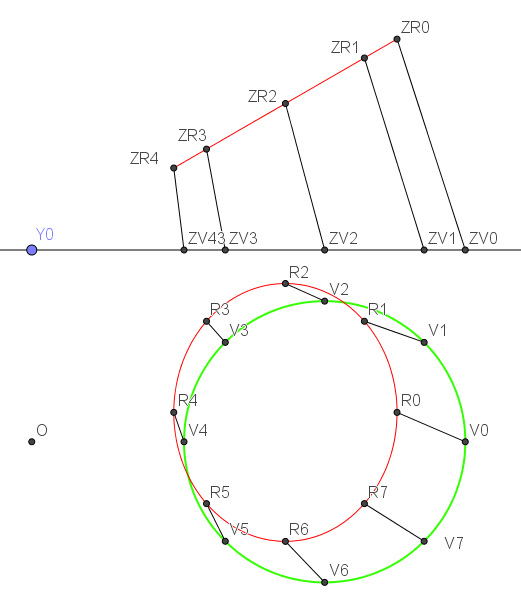
Voici rapidement petite épure du tronçon T4 dont les diamètres de 360 (en vert) et 330 (en rouge) des cercles limites sont donnés dans une table.
Les plans des cercles forment un dièdre d'angle 30°, et ont tous l'axe O1 comme droite commune.
L'axe O1 est ici perpendiculaire au plan frontal et se projette en Y0
le centre de l'ellipse (en rouge) projection du plus petit des deux cercles est bien sûr décalé de 338/9 pour prendre en compte l'hélicoïde sur laquelle se trouvent les centres des cercles
Sur chacun de cercles sont portés 8 points mis en liaison pour préparer un patron d'une surface enveloppante triangulée.
Les calculs des triangles de ce patron sont plus simples à faire par un petit programme (en Python par exemple) mais pourraient découler directement de cette épure.

sauf erreur d'interprétation de cet exercice de BTS tôlerie....

Bonsoir Vham et merci,mais quel tracé
permet de dessiner ce tronçon T4 en vrai grandeur puisque je suppose qu'il ne l'est pas sur la projection frontale?

Cordialement,

Bonsoir,

Qu'appelez-vous "en vrai grandeur" ?
Vous avez des perspectives cavalières dans votre post introductif....
La meilleure vrai grandeur serait peut-être le patron constitué de la suite des triangles par exemple : V0R0R1, V0R1V1, V1R1R2, V1R2V2, ....
Tous ces triangles se tiennent par un côté commun successivement et forment le "patron" de l'enveloppe latérale que l'on peut alors découper sur une tôle plane puis plier...(voir votre exercice précédent : Vrai grandeur de l'angle de pliage)

re bonsoir,oui,mais avant de procéder à la triangulation  il faut connaitre les cotations de chaque tronçons(ils nous donnent simplement les rayons de chaque sections et non les hauteurs,et donc comment faites vous pour les déterminer?

Cordialement,

Bonne nuit,
une épure en géométrie descriptive décrit entièrement la position dans l'espace de chaque point tracé.
Geogebra donne les coordonnées numériques cartésiennes ou polaires à la précision que l'on veut.
Ce sont les calculs numériques effectuées sur les coordonnées des points et sur les équations des courbes qui donnent le tracé.
Mon épure de 16:03 permet donc de calculer la longueur de chaque segment entre deux points déjà tracés, soit en utilisant les coordonnées x, y, z de chaque extrémité, soit en effectuant les rabattements appropriés entre vue horizontale et vue frontale.

Note : je suppose que vous savez trouver la longueur d'un segment entre 2 points quelconques sur une épure en géométrie descriptive
Je suppose aussi que vous savez reproduire l'épure de 16:03.

Oui je comprends ce que vous essayez de m'expliquer, mais ça ne répond pas du tout à ma question.Je pourrais comprendre que   chaque tronçon se projetterait en vraie grandeur sur la projection verticale suivant  un cercle(courbe plane), mais pas un hélicoïde...En revanche j'ai compris comment vous  procédez pour trianguler la surface(même si le sommet est inaccessible),en ce moment j'étudie les surfaces composées(raccordement de section circulaire/ellipse.

Salutations,

Bonsoir,
Pour clore cet exercice voici le patron au 1/100 du tronçon t4
tracé conformément à l'épure du 15-11-18 à 16:03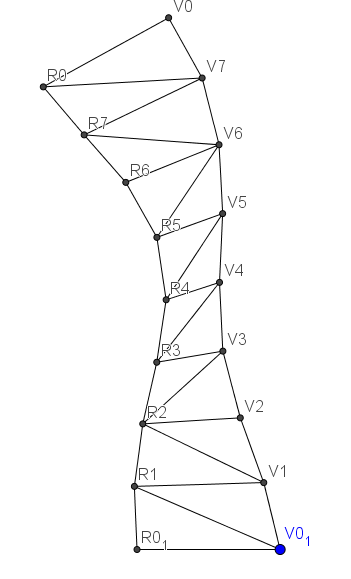

Merci,mais ça ne repond pas à ma question

Bonsoir à vous,quelqu'un peut il m'expliquer comment retrouver les Vraies  grandeurs  des axes de ces cônes ou  bien conoïdes ? Alors,cônes ou conoïde ?
Mathafou:Es tu sur que les sections de ces tronçons sont elliptiques?Tout cela n'est pas très clair!

Cordialement,

en fait si les cônes sont de révolution les sections planes sont des ellipses
mais sinon...
les sections planes d'un cône elliptique pourraient tout à fait être des cercles !
et si ce n'est pas un cône du tout encore plus.
pour ça je donne ma langue au chat.

c'est pour ça que je ne suis plus intervenu après le message de vham 15-11-18 à 16:03 insistant sur une surface développable (au moins par morceaux) qui s'appuierait sur des cercles imposés.

Bonsoir Mathafou et merciAh oui d'accord, tu penserais que la section normale des cônes  ou pas serait elliptique

Et donc pour déterminer la vraie grandeur des axes il faut une troisième vue,de dessus par exemple ?

Cordialement,

imposer que ce soient des cercles suffit.
voir les constructions de vham

Je ne comprends pas la construction de Vham,je le répète, comment détermine on l'axe du tronçon T4 en vraie grandeur, si personne ne  sais et bien c'est que ça n'à pas de sens.

Bonsoir,
L'énoncé qui présente cet exercice de BTS parle bien de géométrie descriptive qu'apparemment, david1972, vous ne maîtrisez pas.
Vous ne semblez pas non plus bien comprendre les plans présentés qui sont des plans de "professionnels".
Alors pour aboutir à ce qui est demandé : "développer chaque tronçon", qu'est-ce qui vous manque ? Voir les notes du 16-11-18 à 00:20

Pour avancer il faut acquérir des connaissances techniques plutôt que se bloquer sur des axes, des cônes ou des conoïdes dont il n'est pas question dans cet exercice

Bon et bien inutile de continuer ,Merci,

Bonjour,

C'est un peu triste de constater comment certains jeunes manquent de détermination à bien progresser, à bien comprendre, à ne pas abandonner sur une difficulté...

Vous dites n'importe quoi,enfin bon,

Salutations,

L'aide est toujours ouverte sur ce forum.
Cordialement

Oui,c'est normal,et puis Merci pour tout de même.J'ai consulter les professionnels de la tôlerie et ils m'ont expliquer les techniques adéquate  pour développer  ces  pièces en fibre neutre.En revanche,chacun son sait que la triangulation est inexacte,donc...

Sincères salutations,

l'inexactitude devient totalement négligeable si on fait tendre le pas de triangulation vers zéro.

après tout c'est bien ce qu'on fait quand on trace une ellipse par exemple : on trace des points isolés et on les relie entre eux !
alors à plus forte raison quand la courbe n'est pas décrite par une équation que l'on connaitrait mais dont on peut tracer (via l'épure) autant de points qu'on veut.

voire un nombre énorme avec un logiciel de géométrie, par exemple avec la fonction "lieu géométrique" de Geogebra.

ici je pense avoir montré que les divers tronçons ne sont pas des troncs de cône de révolution si on impose des sections circulaires.
et j'ai même de forts doutes sur le fait que ce soit des troncs de cônes tout court (elliptiques) à cause de la nécessité qu'il y aurait d'avoir deux directions de plans différentes donnant toutes deux des sections circulaires.

donc "l'axe" je doute que ça ait un sens !!

on effectue donc le développement direct point par point avec un "pas" aussi fin que l'on veut
c'est ce que recouvre la technique de vham avec comme "exemple" un pas de 1/8 de "tour"

Bonsoir Mathafou, d'accord, effectivement  c'est sûrement  des conoîdes,surface dites non développable. Sur mon bouquin ,j'ai un tracé qui permet de le déterminer si l'epure de Vham est exact...Curieux tout de même que ces tronçons ne soit pas développable notament  pour la fabrication comme nous l'avions vu précédemment dans l'étude du coude conique aux sphères tangentes ou  tu m'avais bien aider d'ailleurs. Concernant les axes et selon les professionnels de la tôlerie il suivrait l'hélicoïde suivant des segments de droites. .Enfin cet exercice donne bien du fil à retordre...

Mes salutations à vous,

Voici ce que détermine le tracé permettant d'identifié un tronc de cône ou un conoïde sur le post 15/11 à 16h03  de ce cher Monsieur Vham,lol.
Prolonger les génératrices C,A et DB en S.De S comme centre,je ramène A en a1 et B en b1 la section a1,b1 n'étant pas parallèle à C,D ,c'est un conoïde.
Sincères salutations,
Note, donc c'est non développable

Bonne nuit,

--> david1972 : Si vous ne contestez pas la définition du tronçon T4 telle que je l'ai décrite pour en tracer l'épure du 15-11-18 à 16:03,
ce que vous appelez dans votre dernier post du  17-11-18 à 21:48 :
Genératrice (CA) est, sur mon épure, la projection frontale appelée (ZV4ZR4) d'une droite dont la projection horizontale est la droite (V4R4).
Appelons (D4) cette droite.
Genératrice (DB) est, sur mon épure, la projection frontale appelée (ZV0ZR0) d'une droite dont la projection horizontale est la droite (V0R0).
Appelons (D0) cette droite.

Ce que vous appelez "centre S", intersection de (CA) et (DB) n'est que l'intersection
des projections frontales des droites (D4) et (DO) qui ne se rencontrent pas dans l'espace.

Je ne comprends donc pas l'utilisation que vous faites du point S.
Par ailleurs T4 ne correspond pas à la définition mathématique d'un conoïde et
je me suis appuyé sur une expression analytique paramétrée de la surface de T4
pour développer un patron par triangulation dont je vous assure l'exactitude à 10^-5 près.
  

Si votre image du post 16/11 à 16 h30 est une vue en plan de T4 est bien c'est un conoïde,je m'appui sur le tracé  que j'ai posté 17/11 à 21h48,qui est l'auteur  d'un professeur de l'enseignement technique de Paris. Et apparement, je ne suis pas le seul à penser  que n'est pas des troncs de cônes, donc,c'est du non développable...Et d'après mon expert en tôlerie c'est fabriquer soit par emboutissage ou hydroformage. ..


Cordialement,

Bonsoir,

Depuis tout point de l'arête (O1) du dièdre qui contient les deux cercles de chaque tronçon
(voir l'épure du 15-11-18 à 16:03) on peut mener deux plans tangents aux deux cercles. Ces plans tangents définissent complètement une surface réglée entre les deux cercles.

Les surfaces réglées dont chaque segment de droite est contenu dans un plan tangent sont développables.

Ainsi pour le tronçon T4 de l'épure du 15-11-18 à 16:03 dont j'ai réalisé une maquette (réduite) de sa surface externe développée plane.

Je n'avais pas en mémoire cette propriété quand j'ai proposé une enveloppe triangulée le  16-11-18 à 18:07

Bonsoir,
Vous définissez vos génératrice à l'aide de plans tangents aux cercle,c'est ce que vous expliquez?

Bonsoir,

oui, je définis les génératrices à l'aide de plans tangents aux cercles.
Et je suis certain de la validité du procédé qui utilise un théorème sur les surfaces réglées.
Il est facile de maquetter en réduction pour avoir la forme de la découpe de la surface latérale développée plane.

Bonjour Vham,et bien il est tout à fait possible que vous ayez raison à propos de ces tronçons.J'ai modélisé l'ensemble en C.A.O et donc j'ai vérifié  sur une vue de dessus parallèle à l'axe de l'un des tronçon et oui,la surface est réglée et donc développable dans ce cas.Finalement, pour la fabrication, c'est déjà plus réalisable.Vous souhaitant mes sincères salutations.

Bonsoir,

Les intervenants de ce forum vous aideront toujours au mieux de leurs connaissances. Bonne suite.

Merci,à vous également,

Bien Cordialement,

Bonjour ,

Peut-être pourrions nous intéresser à la pénétration des raccordements non parallèles aux bases circulaires sur le cylindre(virole de diffusion repérée en 3 sur le plan de frabrication)

Cordialement,

Bonjour,

Puisque vous relancez sur cet ensemble bigrement pas facile à étudier, raccordememts entre quoi et quoi Exactement ?
Il serait bien d'avoir une explication sur l'utilisation de cet engin pour pouvoir comprendre ce qui doit être bien défini....

les troncs de cônes qui à mon avis son plutôt des raccordements de deux sections circirculaires non.parallèles .Et donc je cherche à savoir comment définir chaque intersections de ses raccordements avec le cylindre repéré en 3 sur le plan de fabrication.

Cordialement,

Bonsoir,

Je ne peux rien faire concernant la pénétration des raccordememts de l'ensemble "helicoïde" avec la virole centrale "cylindrique" si je n'ai pas d'indication sur le fonctionnement de ce cyclone hélicoïdal...

Bonjour Vham,je ne pourrais vous dire à quoi sert cet ensemble.Mais pourquoi cette question?Dans ce cadre on étudie cet ensemble en géométrie descriptive uniquement donc!

Bonjour,

On ne peut dessiner et avancer que si les données permettent de comprendre avec précision les positionnements respectifs des pièces.
Je me retire donc de cette discussion.