Inscription / Connexion Nouveau Sujet
Dans un repère
Bonjour voici mon sujet:
Dans l'espace, on se fixe un repère (O ;  ;
;  ;
;  ). On se place dans le cube unité comme ci-dessous.
). On se place dans le cube unité comme ci-dessous.
1. Représenter l'ensemble des points M(x ; y ; z) vérifiant:
0 x
x  1
1
0 y
y  1
1
0 z
z  1
1
x+y+z  1/2
1/2
2.Quel est le volume du solide obtenu, (l'unité de volume étant le volume du parallélépipède unité hérité de la base choisie).
3. Soient trois nombres sont pris au hasard dans l'intervalle [0;1], indépendamment les uns des autres. Démontrer que la probabilité pour que leur somme soit inférieur ou égale à 1/2 vaut presque 2%.
Merci d'avance pour votre aide.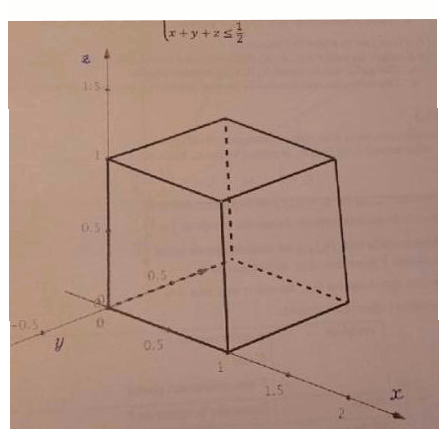
malou > ***image tournée***
Bonjour,
x+y+z = 1/2 est l'équation d'un plan
x+y+z < 1/2 est la partie de l'espace de même côté de ce plan que l'origine (parce que 0 + 0 + 0 < 1/2 montre que O appartient à la région de l'espace concernée)
il s'agit donc de tracer ce plan et son intersection (section) avec le cube, deja, histoire de voir à quoi ça ressemble, ce solide mystère.


