Inscription / Connexion Nouveau Sujet
dans un trapeze ABCD ....
voici un exercice avec lequel je me bat depuis une heure sans réussir a m'en sortir je me sui donc accroché a la possibilité qu'un forum de maths pourrait m'aider merci d'avance ( je suis bloqué au 1) )
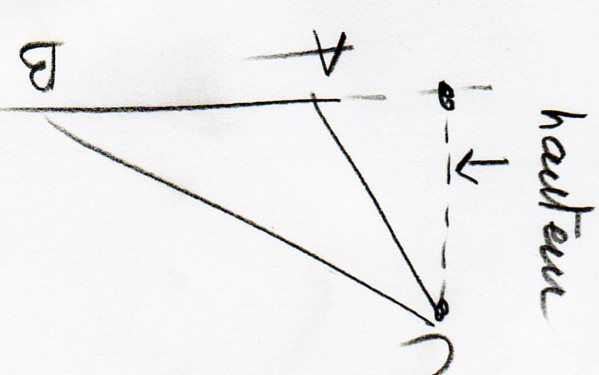
ABCD est un trapeze de bases (AB) et (CD) .
On note h sa hauteur.
Le point A' est le projeté orthogonal de A sur (BC).
Le point B' est le projeté orthogonal de B sur (AD).
1)démontrer que les triangles ABD et ABC on la même aire
2)en déduire que : BC/AD = BB'/AA'
3)on suppose que le trapeze ABCD est rectangle en A démontrer alors que: AA'= AB*AD/BC
je suppose que tu as fait le dessin l'aire de ABC est AB 
h/2
et l'aire de ABD est AB h/2
conclusion : ...?
pour la deuxième question...
il y a une autre façon de calculer les aires ..
l'aire de ABC est : BCAA'/2
l'aire de ABD est : ADBB'/2
or ces deux aires sont égales
donc BCAA'/2 = ADBB'/2
en "supprimant" les /2
on a BCAA' = ADBB'
donc BC/AD = BB'/AA'
oui je connais mes fomules (du moins celles-ci) mais le problème c'est que h n'est pas la hauteur de ABC
ni de ABD et je n'ai pas leur hauteurs respecives
tu rigoles ou t'es sérieux quand tu écris : "mais le problème c'est que h n'est pas la hauteur de ABC ni de ABD et je n'ai pas leur hauteurs respectives " ???
souviens toi de ta sixième ... il n'y avait pas des hauteurs qui "n'etaient pas" dans le triangle mais à l'extérieur????
mea culpa pour les hauteurs 
Annuler
connectez vous