Inscription / Connexion Nouveau Sujet
Demonstration d'une formule trigonométrique
Bonsoir 
On me donne tan(x) = et les formules sin (a+b) et cos (a+b).
Il est marqué : La fonction x -> cos x est paire ; la fonction x -> sin x est impaire.
Question : Etablir la formule donnant tan(a-b) en fonction de tan a et tan b.
J'ai :
tan(a-b)= =
Mais je ne comprend pas après comment on arrive à
tan(a-b) =
J'ai trouvé cette demonstration en surfant sur Internet...donc je ne sais pas si ça correspond à ce qui est demandé.
En esperant que quelqu'un éclaire ma lanterne.
Voila
Merci d'avance.
Ah oui, désolée, oublie du moins (merci disdrometre) :
tan(a-b) =
Mais je ne comprends toujours pas comment on en arrive là...
non !!
au numératueur sin(a)cos(b) - sin(b)cos(a) = cos(a)cos(b)(tan(a) -tan(b))
au dénominateur cos(a)cos(b) + sin(a)sin(b) = cos(a)cos(b)(1+tan(a)tan(b))
on simplifie par cos(a)cos(b) et on trouve le résultat
D.
Re-bonsoir
Je coince encore pour une question (suite de l'exercice) :
Enoncé :
A quelle distance doit-on se placer de l'écran pour avoir le meilleur angle de vision possible ?
Le repere est orthonormé.
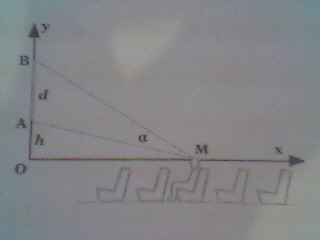
[AB] est l'écran, vu de profil. M est l'oeil du spectateur
OA=h ; AB=d ; OM=x ; 
= mesure de AMB en degrés.
1.Exprimer tan et tan
en fonction de d, h et x
En déduire que tan=
2.Pour alléger les calculs, on pose : h(h+d)=a².
Etablir le tableau de variation de : x-> tanest maximum.
(On admettra que la fonction tangente est strictement croissante)
En déduire la valeur de x pour laquelle l'angle
On prend h=2m et d=2,5m. Calculer la valeur de x pour laquelle est maximale.
De combien peut-on s'écarter de cette valeur sans que s'écarte de plus de 15% de son maximum ?
Voila
Je bloque au 2 ...
Merci d'avance
Bonjour,
Pour répondre à la question 2, il te faut étudier la fonction f sur [0 ; +oo[ définie par f(x) = d x / (x² + a²), c'est à dire étudier ses variations (croissante puis décroissante) en ayant étudier le signe de sa dérivée f'(x).
Tu devrais en déduire que cette fonction admet un maximum (f(x) maximum) en x = a.
....
Annuler
connectez vous