Inscription / Connexion Nouveau Sujet
Démonstration en fonction d'un triangle
Bonsoir à tous, je suis actuellement perdu dans un exercice de géométrie.
Je suis actuellement en classe de seconde générale.
J'ai essayer de donner le plus d'informations venant de ma part, histoire de montrer que je veux vraiment réussir et comprendre.
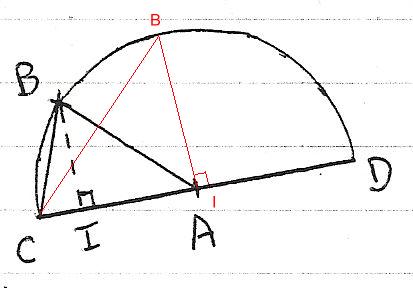
Voici un schéma que je vous ai refait, le trait vert, et rouge, c'est moi qui les a fait :
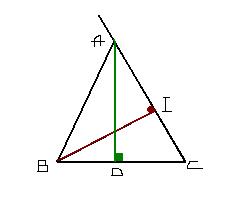
Voici le sujet + mes réponses :
On se propose dans cette question de trouver la valeur exacte de x0.
On a tracé le demi-cercle "C" de centre A et de rayon AC.
B est un point de "C" et I le projeté orthoonal de B sur (AC).
A) Démontrer que Aire(ABC)=4xBI
# I étant le projeté orthogonal de B sur (AC) donc (BI) est perpendiculaire à (AC).
# On nomme D un point correspond au pied de la hauteur issue de A de ce triangle.
# Aire de ABC = (base x hauteur)/2 = (BC x DA)/2
B) L'aire du triangle ABC est maximale lrosque BI est maximale. Quelle est la position de B sur "C" pour qu'il en soit ainsi ?
# La position de B est toujours inscrit sur le cercle "C" et doit être aligné avec A,I,C, afin que BI soit au maximale.
C) En déduire que le triangle BAC est rectangle isocèle en A et que x0=8(racine)2
# Pour qu'il soit isocèle rectangle, il faut qu'il est :
# # un angle droit donc il faut que (CA) soit perpendiculaire à (BA)
# # deux côtés égaux, donc que [AB]=[AC], or ce sont des rayons du cercle donc ils sont égaux.
Merci d'avance 
pracc13.
Bpnsoir . Tu es en Première (profil ?) ou en Seconde , comme tu le dis ici ?
On n'a pas tout l'énoncé , c'est difficile de te répondre, car on ne connait pas toutes les données !...
Tout cela semble bon , quand même, mais la remarque de la question B " le point B doit etre aligné avec A, I, C,..." me parait curieuse .
Comment est défini xo ?...
Bonsoir,
A)
aire ABC = AC*BI/2
aire ABC = 8*BI/2
aire ABC = 4*BI
B)
le point B se déplace sur le cercle
BI est maximum quand il est égal au rayon donc à AC et AB
BI est confondu avec AB
le triangle ABC est rectangle en A
C)
BC est l'hypoténuse d'un triangle rectangle isocèle de côté 8
BC = 8 2
2  11,3137
11,3137
Désolé, j'ai utilisé le compte de mon cousin qui lui est en première 
Daniel62 : Merci, mais pourrais-je avoir plus de renseignement afin de mieux comprendre, et
ABC est un triangle isocèle tel que : AB = AC = 8 cm et BC = x cm
que veux tu savoir ?
A) aire = base*hauteur/2 = AC*BI/2 = 4BI
B) aire est maximale quand BI est maximal
le point B à la vertical de A
I est confondu avec le point A
BI = BA = rayon = 8
ABC est rectangle isocèle en A
aire = 4*BI = 4*8 = 32
Merci beaucoup de ta part !!
Je vais regarder tout cela demain au calme, en cas de problème je te ferai signe.
Bonne soirée !!