Bonjour,
se rappeler qu'une suite géométrique converge si sa raison en valeur absolue est inférieure à 1 et diverge sinon (et stationnaire si la raison = 1)
réfléchis à ce que ça implique pour les Z_n

Bonjour,

La suite fait intervenir des nombres complexes.
Est ce que la formule d'Euler te dis quelque chose?

Peu importe, dans ton cas la raison est positive. Donc si elle est entre 0 et 1 la suite converge et si elle est plus grande que 1 la suite diverge.

Si tu n'as pas vu la formule d'Euler tu ne peux pas traiter l'interprétation géométrique ...



ça ne te dis vraiment rien?


la fonction valeur absolue ne te dis rien non plus?

euh pour la valeur absolue, l'une des inégalité n'est pas stricte, dsl. donc

Oui je suis sûr et certain de ne jamais avoir vu cette formule... Donc ici comme la raison est positive et comprise entre 0 et  1 la suitee converge ?

Mais dans ce cas si la suite converge elle va converger vers 0, dans l'exercice il faut l'interpréter géométriquement, peut on donc dire que la courbe représentative de la fonction Rn va se rapprocher de 0 ?

Bonjour, je suis bloqué sur une question que je n'arrive pas à faire et à traduire, je me permets d'envoyer le sujet car celui ci possède des signes que je ne peux pas reproduire au clavier

Je suis bloqué à la question 4a, je ne comprends vraiment pas par où commencer

** image supprimée **

*** message déplacé ***

Bonjour
pour avoir le droit de mettre ton sujet en image, tu dois recopier au moins tout le début, qu'on puisse retrouver le sujet
tu n'oublieras pas non plus de donner ce que tu as fait

extrait de la FAQ du forum :

Q10 - Puis-je insérer des symboles mathématiques afin de faciliter la lecture de mon message ?

Oui, cela est même encouragé.

Les correcteurs sont généralement plus attirés par un message bien écrit en Latex et bien présenté que par un message écrit avec les caractères normaux, non aéré, etc.

Le Latex est un outil mathématique qui pouvait nous permettre à tous de faciliter la lecture et la compréhension en écrivant proprement nos formules mathématiques. Nous vous invitons à prendre connaissance du guide latex présent sur le site. Un tutorial complet vous aide à faire vos premiers pas.
Bien-sûr, l'utilisation du Latex n'est pas obligatoire, mais pourquoi se priver d'un tel outil ?

Si ce langage vous semble trop compliqué à utiliser dans un premier temps, il vous est cependant possible d'insérer très simplement des caractères mathématiques dans votre texte en utilisant l'outil présent sous la zone de saisie du message. La liste complète des caractères mathématiques est disponible dans le mode d'emploi du forum.

extrait de la FAQ du forum :

Q05 - Puis-je insérer une image dans mon message ? Comment faire ? Quelle image est autorisée ?

Vous souhaitez ajouter une image ou un pdf à votre message . Veuillez obligatoirement respecter ces règles :

Énoncé d'exercice ou de problème :

Pour les énoncés courts (moins de 5 lignes sur une feuille A4) :
La recopie est obligatoire.
L'option d'attachement d'image n'est donc à utiliser que pour représenter une figure, un tableau ou un graphique, pas du texte !

Pour les énoncés longs  :
Les 5 premières lignes sont à recopier pour aider l'archivage des sujets sur le site.
Cela fait, l'énoncé dans sa totalité, pourra alors être joint en image (choisir Img) ou en pdf (choisir Pdf ) mais dans le respect des droits d'auteurs en vigueur. Pour les pdf, merci d'en préciser la source.

Recherches (même non abouties) de l'exercice :
Elles doivent être obligatoirement recopiées, et ce, dès la demande d'aide.
l'option d'attachement d'image n'est donc à utiliser que pour représenter une figure, un tableau ou un graphique, pas du texte !
Les formats autorisés sont exclusivement les suivants : gif, jpg, jpeg, et png. La taille d'un fichier est limitée à 2 MO maximum pour une image et à 500 ko pour un pdf.

Le non respect de ces règles entraînera la suppression du contenu de votre sujet (même si des réponses ont été apportées) et éventuellement la suspension de votre compte !

Seule exception : Dans le forum détente, des réponses longues et élaborées , contenant plusieurs images explicatives, pourront être postées sous forme d'image ou de pdf. Les énoncés, quant à eux, devront toujours être rédigés sur le site (indispensable pour le référencement).

D'accord
Donc on note Ln  la longueur de la ligne brisée qui relie le point An en passant succesivvement par les points A1 A2 A3 etc
Ainsi Ln =     n-1
                         Sigma * Ai Ai+1 = A0A1 + A1A2 + A2A3 + ... + An-1 An
                              i= 0
pour tout entier naturel n non nul

a) démontrer  que pour tout entier naturel n  AnAn+1 = Rn+1



Voici le sujet pour vous y retrouver plus facilement, il s'agit de la question 4 a



*** message déplacé ***

Je ne vois pas du tout comment faire et par où commencer

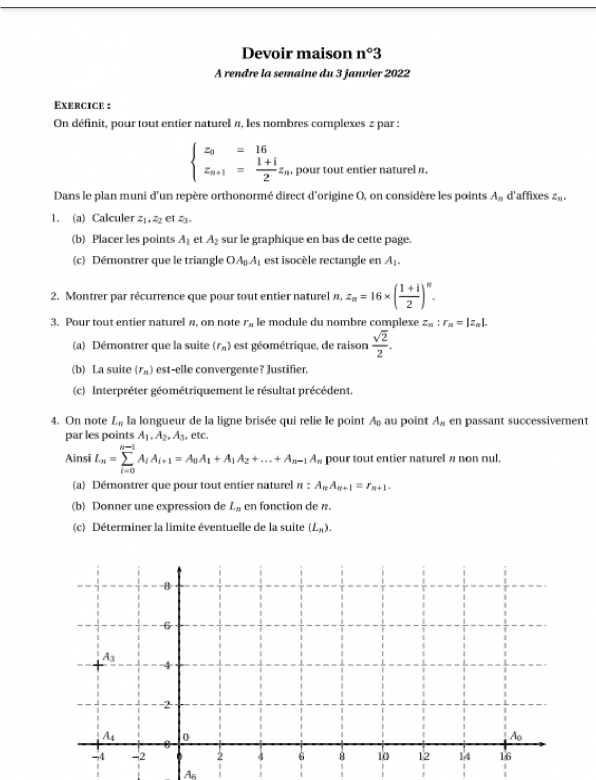
*** message déplacé ***

toutes les questions d'un même problème doivent être posées dans le même sujet !

tu m'étonnes de ne pas savoir le faire si tu fais abstraction de tout ce qui a été fait avant !
c'est bien pour cela que je demandais au moins les résultats aux questions précédentes

D'accord désolé mais du coup est-ce possible d'avoir de l'aide svp ?

je suis déjà beaucoup de sujets...

un dépannage

tu connais l'affixe de A_n et celle de A_n+1

donc tu peux calculer la distance A_nA_n+1

Je ne vois pas quelle est l'affixe de An et An+1..

relis ton énoncé, c'est écrit dedans !

An+1 = ((1+i)/2)*An
et An = 16* ((1+i)/2)^n  ?

attention...ne pas confondre un point et son affixe, ce n'est pas égal

Et donc pour obtenir la distance il faut faire
((1+i)/2)*An -  16* ((1+i)/2)^n ?

je crois que tu essaies de faire ton exercice sans avoir appris ton cours
ça ne peut pas aller
distance entre 2 points = module d'une différence d'affixes

J'ai appris mon cours mais je ne vois vraiment pas quel calcul il faut faire je comprends ce qu'est un module mais je ne vois pas quel calcul il faut faire exactement quelle est l'affixe ici svp ?

l'affixe de A_n est (voir ton énoncé)
l'affixe de A_n+1 est (voir ton énoncé)

donc A_nA_n+1= module de la différence des deux affixes écrites

tout simplement

donc le calcule à faire est
    | ((1+i)/2)-16* ((1+i)/2)^n - 16* ((1+i)/2)^n | ?

bonjour à tous

malou, si je dis une bêtise, n'hésite pas à me reprendre.

4a) je tiens compte de la question 1c), qui attire l'attention sur une particularité des triangles  OA_nA_n+1
(on peut facilement démontrer sa généralisation par récurrence)

ensuite, à l'aide de la question 3) ça roule tout seul.

_{*modération* >citation inutile supprimée*}


Merci pour votre réponse, donc on sait que rn+1 = |zn+1| donc |zn+1| = AnAn+1

De plus on sait que Rn+1 = ?2/2 Rn


On sait que la suite Rn va se rapprocher de  0, mais donc je ne vois toujours pas comment calculer le module de la différence des affixes.. Serait-il possible de me mettre les premières lignes de calculs pour que je puisse comprendre lequel faire s'il vous plaît ?

donc |zn+1| = AnAn+1     ---  non, c'est justement ce que tu dois démontrer
...revois la définition d'un module, j'ai l'impression que ce n'est pas clair pour toi :
r_n = |z_n| = OA_n

merci de ne pas citer les messages, qui alourdissent le fil.

petit dessin pour argumenter mes propos précédents :

d'accord merci mais du coup je ne comprends toujours pas quels calculs effectuer, pourriez vous rédiger juste le début du calcul pour que je puisse comprendre svp ?

en l'absence de Malou, qui reprend la main dès qu'elle le souhaite.

on va poursuivre la piste donnée par Malou :

Affixe de An : (1/2) +(1/2)i
An+1 : 16*1/2 +16*i/2 ?

mais non, tu compliques inutilement,  et surtout je me demande où tu as lu ça.

énoncé : 2ème phrase : l'affixe de A_n est z_n
donc  l'affixe de A_n+1 est z_n+1

ensuite : cours  - qu'il faut apprendre
Soient A et B deux points du plan complexes d'affixes respectifs zA et zB.
La distance AB est le module du nombre complexe zB - zA :
                                         AB=|zB - zA|


donc, ici, distance A_nA_n+1 = .............?

ensuite, on utilise la question 2)...

à toi