Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale IntégrationTopics traitant de Intégration [tout]Lister tous les topics de mathématiques
Niveau terminale
Partager :

Démontrer la formule de l'aire d'une sphère

Posté par
athrun 27-05-10 à 19:03

Bonsoir,

je veux démontrer la formule de l'aire d'une sphère, à savoir 3$4\pi R^2, où 3$R est le rayon de cette sphère.

Je pars donc d'une fonction 3$f définie sur 3$\rm{[-R;R]} définie par 3$f(x)=\sqrt{R^2-x^2}.

L'aire 3$A de la sphère est donc, si je ne me suis pas trompé :

5$\fbox{A=2\pi\Bigint_{-R}^R\sqrt{R^2-x^2}dx}


Pouvez-vous me donner des astuces pour parvenir à calculer cette intégrale ?

J'ai vu qu'on pouvait effectuer des changements de variable...


merci d'avance

Posté par
cailloux Correcteurre : Démontrer la formule de l'aire d'une sphère 27-05-10 à 19:12

Bonjour,

Es-tu sûr du coefficient devant l' intégrale ?

Sinon, pour l' intégrale proprement dite, il s' agit de l' aire du domaine limité par le demi cercle supérieur de rayon R et de centre O et l' axe des abscisses:

y=\sqrt{R^2-x^2} \text{ soit} \{x^2+y^2=R^2\\y\geq 0

Posté par
ZULUSSREALMre : Démontrer la formule de l'aire d'une sphère 27-05-10 à 19:16

oui tu peux faire des changements de variables ,
tu poses x²=Y,il faudrait que tu calcuke l'intégrale sur -R;0 et sur 0;R
mais connait tu le changement de variable pour des intégrales?

Posté par
athrunre : Démontrer la formule de l'aire d'une sphère 27-05-10 à 19:20

Bonsoir Cailloux merci pour ta réponse.



en fait je calcule la somme des périmètres des cercle de rayon f(x), c'est-à-dire 3$\int_{-R}^R2\pi f(x)dx

Ensuite l'intégrale doit alors valoir \frac{1}{2}\pi R^2 ce qui me donne \pi^2R^2 comme aire ..

Posté par
athrunre : Démontrer la formule de l'aire d'une sphère 27-05-10 à 19:22

Bonsoir, ZULUSSREALM, les intégrales sur [-R;0] et [0;R] sont égales. Un changement de variable est toujours un changement de variable, non ? C'est particulier pour les intégrales ?

Posté par
cailloux Correcteurre : Démontrer la formule de l'aire d'une sphère 27-05-10 à 19:27

Oui et c' est faux, tu as commis une erreur:

Une "somme" de périmètres ne donne pas une aire.

Je ne sais pas si tu peux y parvenir de cette manière.

En tout cas, la méthode standard consiste à passer en coordonnées sphériques avec \varphi "longitude" et \theta latitude.

Un élément d' aire vaut alors R^2\,\cos\,\theta\,\text{d}\theta\,\text{d}\varphi

Puis à calculer une intégrale double relativement simple.

Posté par
Priamre : Démontrer la formule de l'aire d'une sphère 27-05-10 à 19:28

Tu pourrais essayer le changement de variable  x = Rsint.

Posté par
athrunre : Démontrer la formule de l'aire d'une sphère 27-05-10 à 19:30

Citation :
Une "somme" de périmètres ne donne pas une aire.


Voilà. Mon raisonnement initial était faux ^^


Merci pour les coordonnées sphériques je vais voir ce que c'est.
Sinon ça peut se faire en coordonnées polaires aussi ?

Posté par
cailloux Correcteurre : Démontrer la formule de l'aire d'une sphère 27-05-10 à 19:35

Sur une sphère, il est tout de même normal d' utiliser des coordonnées ... sphériques.

Mais de toute manière, dans l' espace, des coordonnées polaires sur une sphère sont des coordonnées sphériques puisque OM=R

Posté par
cailloux Correcteurre : Démontrer la formule de l'aire d'une sphère 27-05-10 à 20:59

On peut tout de même s' en tirer comme ceci:

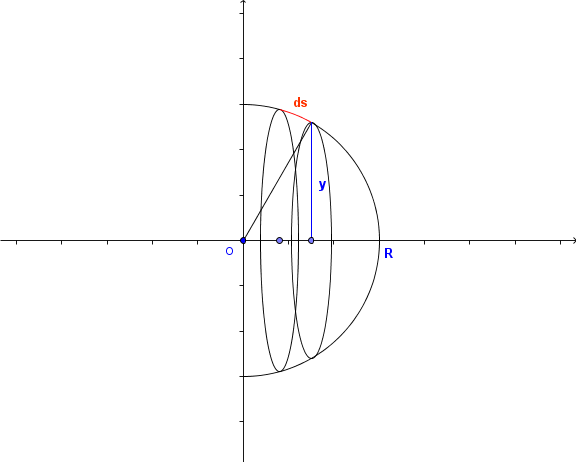
Démontrer la formule de l\'aire d\'une sphère

L' élément de surface de sphère entre les deux parallèles:

dS=2\pi\,y\,ds

avec ds^2=dx^2+dy^2=(1+y'^2)dx^2

ds=\sqrt{1+y'^2}dx et y=\sqrt{R^2-x^2}

y'=-\frac{x}{\sqrt{R^2-x^2}}

y\,ds=Rdx

\frac{S}{2}=\Bigint_0^R 2\pi R\,\text{d}x=2\pi R^2

S=4\piR^2

Posté par
Priamre : Démontrer la formule de l'aire d'une sphère 28-05-10 à 08:14

Ainsi, athrun confondait dx et ds.

Posté par
athrunre : Démontrer la formule de l'aire d'une sphère 28-05-10 à 18:52

Ah il faut donc utiliser un ds ... on les utilise pas pourtant dans le calcul du volume (de la sphère) ?

Citation :
Ainsi, athrun confondait dx et ds.


En fait c'est pas que je confondais c'est que je connaissais pas ds ^^

Si j'ai bien compris, dS correspond à un bout d'aire (grossièrement un périmètre large, une bande) ?

et le ds c'est un dx courbé ?


merci en tout cas

Posté par
cailloux Correcteurre : Démontrer la formule de l'aire d'une sphère 28-05-10 à 19:41

Citation :
Si j'ai bien compris, dS correspond à un bout d'aire (grossièrement un périmètre large, une bande) ?


Oui, à l' aire d' un rectangle de longueur 2\pi y et de largeur ds

Citation :
et le ds c'est un dx courbé ?


Si tu veux; c' est plutôt une longueur élémentaire sur une courbe:

considère un triangle rectangle élémentaire dont l' hypothénuse vaut ds et donc les côtés de l' angle droit son parallèles aux axes de coordonnées.

Ces côtés de l' angle droit valent dx et dy en valeur absolue.

Si bien qu' avec Pythagore, ds^2=dx^2+dy^2

Pour une courbe, on considère qu' un ds est la longueur d' un segment de droite élémentaire.

si y est une fonction de x:

dy=y'dx

d' où ds=\sqrt{(1+y'^2)}dx

Tout ceci est très visuel et pas très "mathématiques"; c' est juste pour que tu aies une vue pratique des choses à la physicienne.

Posté par
athrunre : Démontrer la formule de l'aire d'une sphère 28-05-10 à 20:58

Merci pour ton commentaire ça éclaire pas mal de choses ...

on assimile donc ds à un segment (d'où le élémentaire) puisque c'est une longueur infinitésimale.

Ensuite, \frac{dy}{dx}=y' oui ça je connais


Donc en fait, l'intégrale correcte, que j'aurais du écrire dans mon premier post était en fait :



4$\fbox{S=2\pi\Bigint_{-R}^R\sqrt{R^2-x^2}ds}

le calcul de ds simplifiant tout.

Donc en gros si j'ai bien compris si on prend ds et pas dx c'est parce qu'il y a une variation en y en plus de celle en x ?


Eh bien merci beaucoup Cailloux en tout cas

parce que les coordonnées sphériques je les ai trouvées assez compliquées ...

Posté par
athrunre : Démontrer la formule de l'aire d'une sphère 28-05-10 à 21:05

le schéma est superbe à propos, ça représente très bien.

Posté par
cailloux Correcteurre : Démontrer la formule de l'aire d'une sphère 28-05-10 à 21:37

Citation :
4$\fbox{S=2\pi\Bigint_{-R}^R\sqrt{R^2-x^2}ds}


Oui, autant écrire S=2\pi\Bigint_{-R}^Ryds

Posté par
athrunre : Démontrer la formule de l'aire d'une sphère 28-05-10 à 21:38

Héhé oui je l'ai écrit de ma façon car ça a plus de gu.... ^^

Posté par
cailloux Correcteurre : Démontrer la formule de l'aire d'une sphère 28-05-10 à 21:39

Quant au schéma, je n' étais qu' à moitié satisfait.

Je n' ai pas encore trouvé le moyen de dessiner simplement des demi ellipses avec Geogebra.

Posté par
bamboumre : Démontrer la formule de l'aire d'une sphère 28-05-10 à 21:56

En coordonnées spheriques ca marche:
dS = R2sindd = R2sin dd
avec 0<< et 0<<2
Ce qui fair R2(cos0-cos)2 donc 4R2

Posté par
athrunre : Démontrer la formule de l'aire d'une sphère 28-05-10 à 21:59

Ah tu ne voulais pas qu'on voit la partie de l'ellipse "derrière".

En tout cas tu maîtrises bien le logiciel.

Posté par
athrunre : Démontrer la formule de l'aire d'une sphère 28-05-10 à 22:01

merci bamboum pour ta démonstration avec les coordonnées sphériques même si je n'y ai rien compris ^^

Posté par
cailloux Correcteurre : Démontrer la formule de l'aire d'une sphère 28-05-10 à 22:03

Citation :
Ah tu ne voulais pas qu'on voit la partie de l'ellipse "derrière".


Tout à fait (ou alors en pointillé) mais je ne sais pas comment m' y prendre

Posté par
athrunre : Démontrer la formule de l'aire d'une sphère 28-05-10 à 22:21

peut-être est-ce impossible si ça se trouve ..


Rechercher
Menu
Espace membre
11 visiteurs
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1727 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !